神经网络基本概念
相关练习项目:一个简单的神经网络
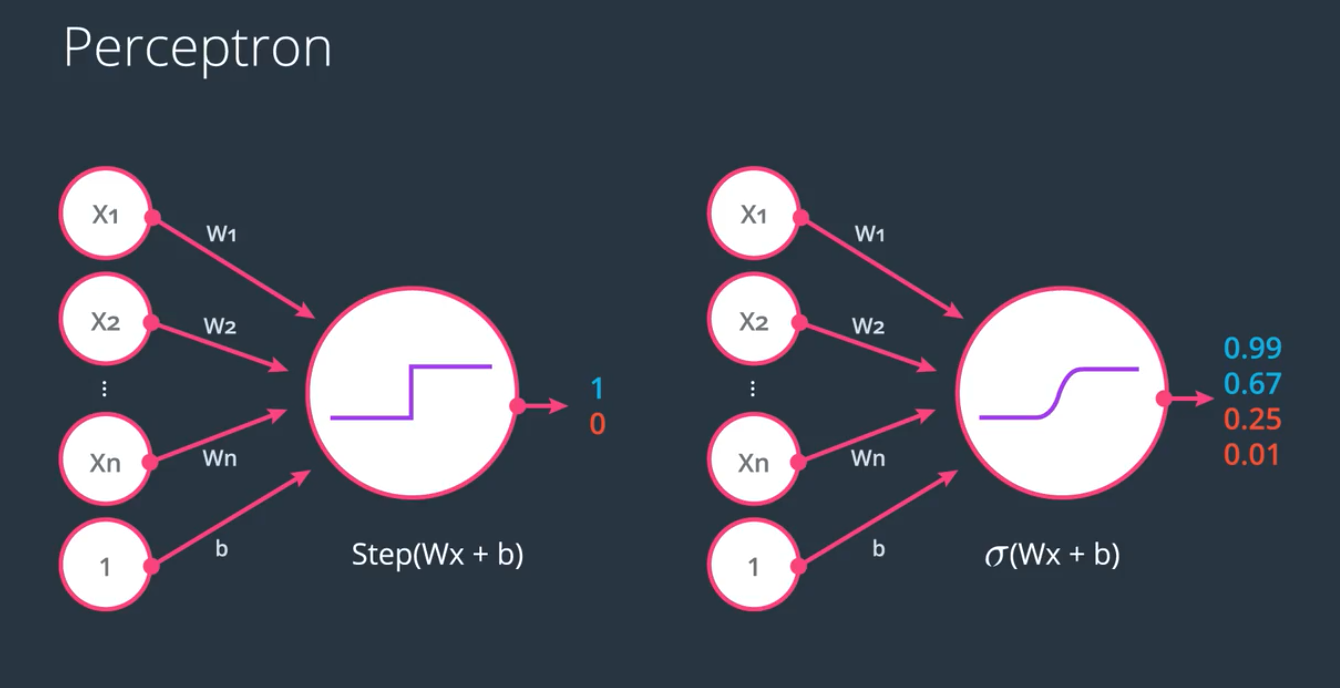
感知器 (perceptron)
即信号输入元, 单个的数据源, 比如人的眼睛,耳朵,鼻子,都是感知器
离散型和连续型预测 (discrete & continuous)
激活函数 (activation function)
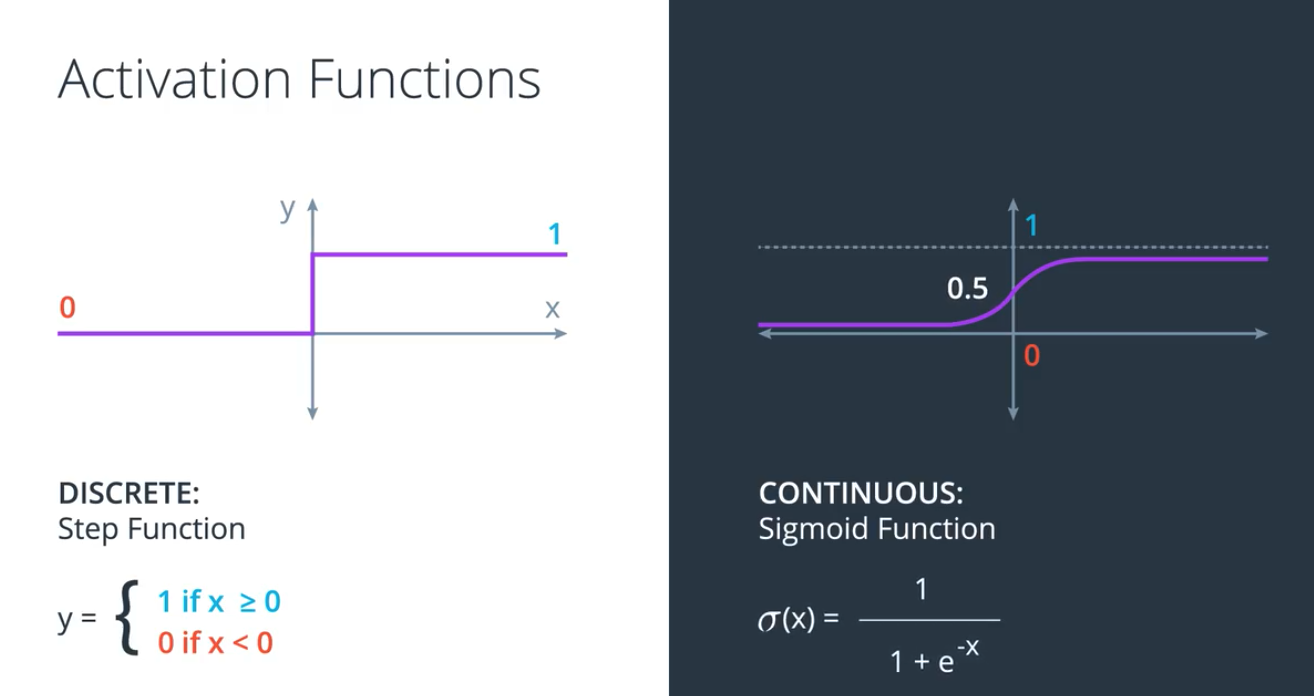
使用连续激活函数,预测的结果不是非对即错,而是一个概率,表示预测结果的可靠,及确定性
SoftMax
多类别分类时使用 SoftMax

定义
def softmax(L):
expL = np.exp(L)
return expL/expL.sum()
分类问题的预测结果使用softmax作为激活函数,转化之后的结果加总为 100%,每个值代表一个预测结果可能发生的概率
One-hot Encoding
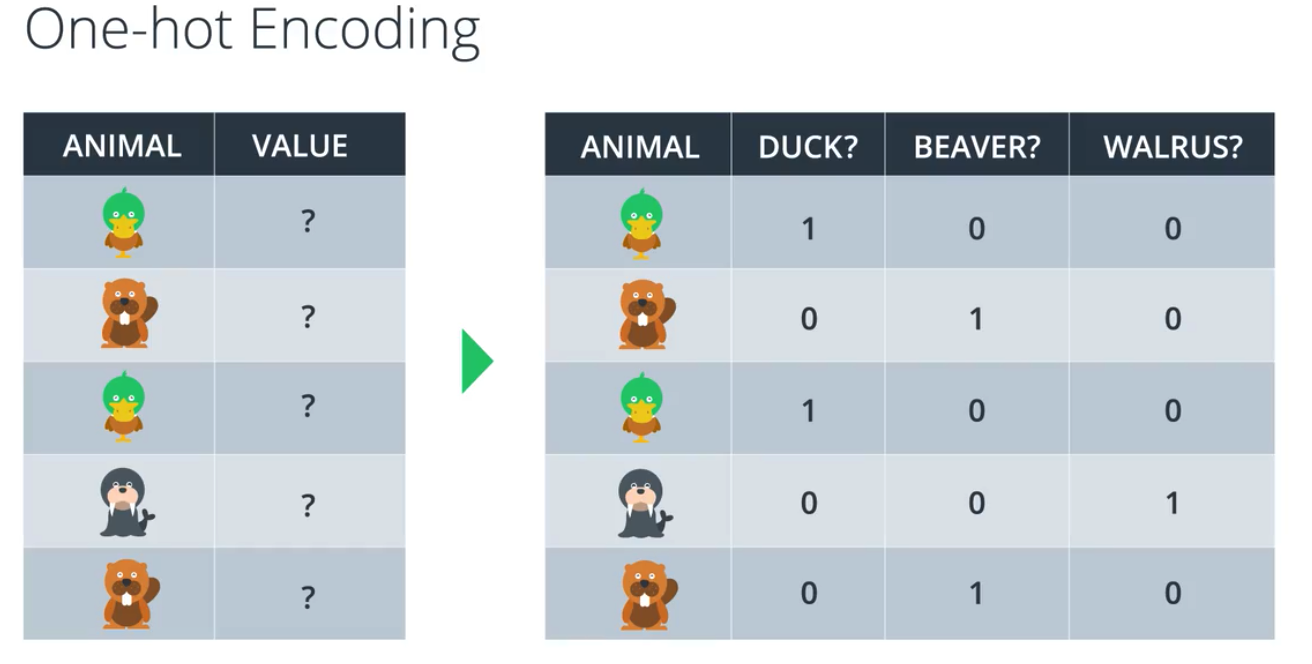 多类别分类时,分类目标数据一般表示为
多类别分类时,分类目标数据一般表示为[2,4,56,7,8,...],需要转换成类似
[[0,1,0,0,0,0,0],
[0,0,0,1,0,0,0],
[0,0,1,0,0,0,0],
[0,0,0,0,1,0,0],
...]
这样的数据,计算机才能高效的处理.
(不过使用PyTorch做分类问题时,不需要手动转化)
最大似然率(maximum likelihood)
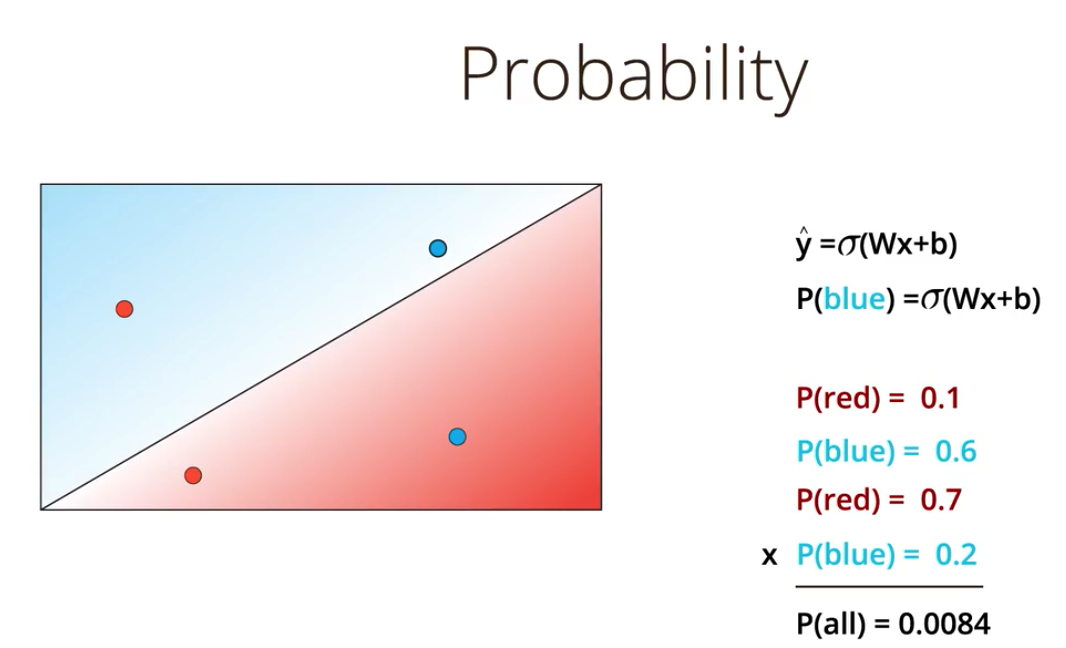 最大似然率 所有预测结果(概率)的乘积, 用来衡量预测的结果的好坏,随着数据量变大,乘积无限接近0,不是一个好的衡量方式,所以不用.
最大似然率 所有预测结果(概率)的乘积, 用来衡量预测的结果的好坏,随着数据量变大,乘积无限接近0,不是一个好的衡量方式,所以不用.
交叉墒(cross entropy)
概率和误差函数之间有一定的联系,这种联系叫做交叉墒
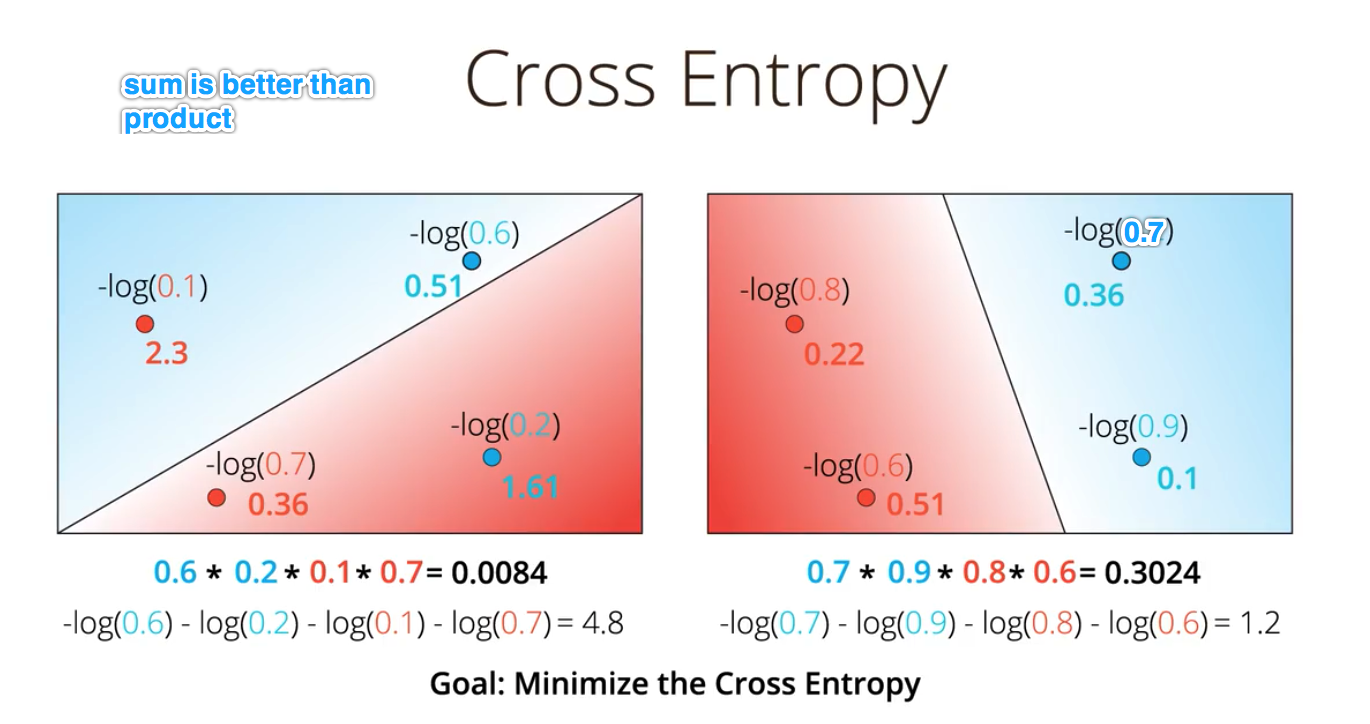
把每个预测概率转化成 对数(-log)并相加,可以很方便的求均值,因此这个误差函数不管数据量的大与小,都有比较好的参考价值

多类别交叉墒(Multi-Class Cross-Entropy)

误差函数(Error function, criterion)
 交叉墒误差函数:
交叉墒误差函数:
👈左边为二元分类问题的误差函数,👉右边为多元分类问题的误差函数,
其他误差函数还有均方差(MSE),L1,kl,详见here
神经网络架构
对现实世界的复杂问题,一般不能用二分法进行分类预测,根据实际问题数据集分布情况,采用不同层级的网络结构才能得到比较好的预测结果.
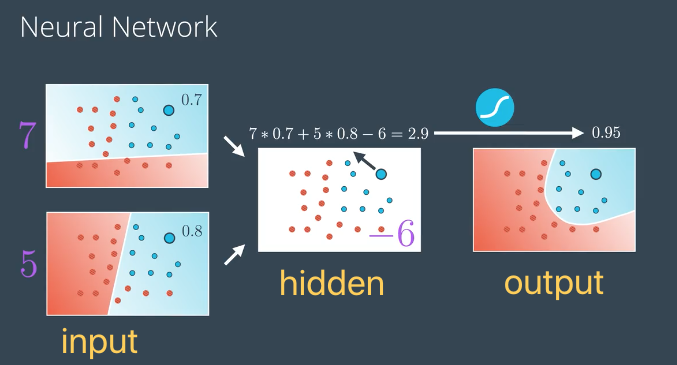
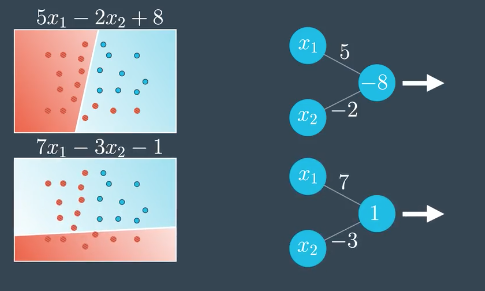
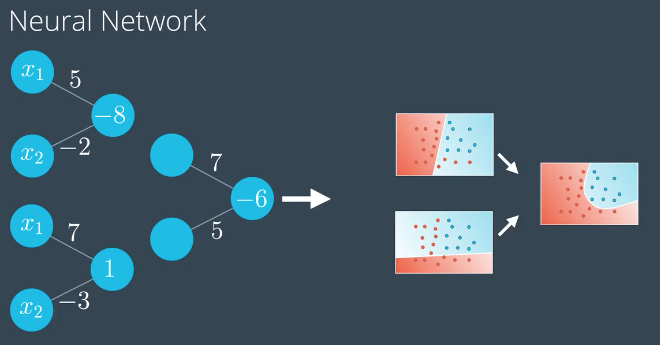
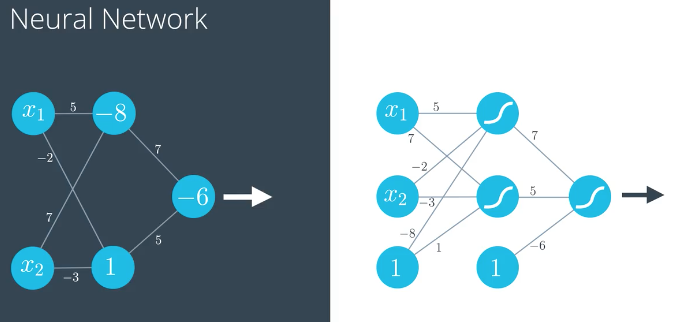
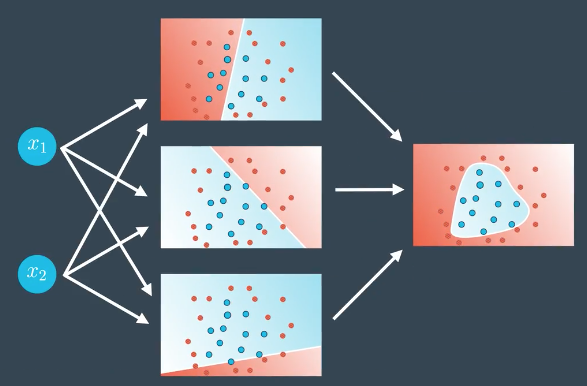
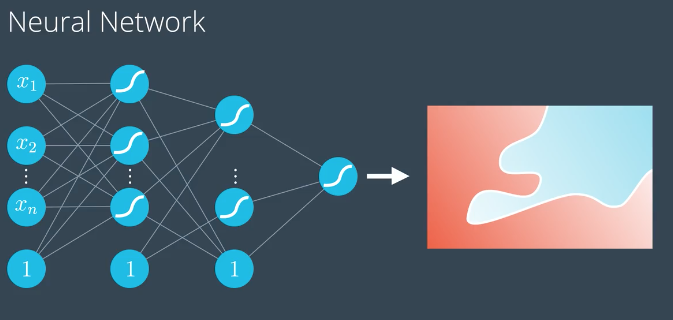
多类别分类
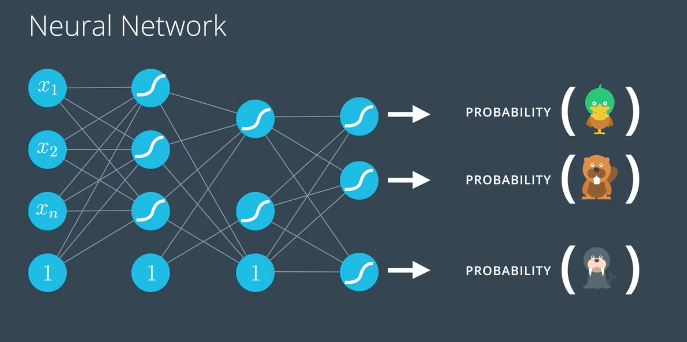 输出层使用 softmax作为激活函数,预测不同类别的概率
输出层使用 softmax作为激活函数,预测不同类别的概率
前向反馈 (feedforward)
前向反馈是神经网络用来将输入变成输出的过程.
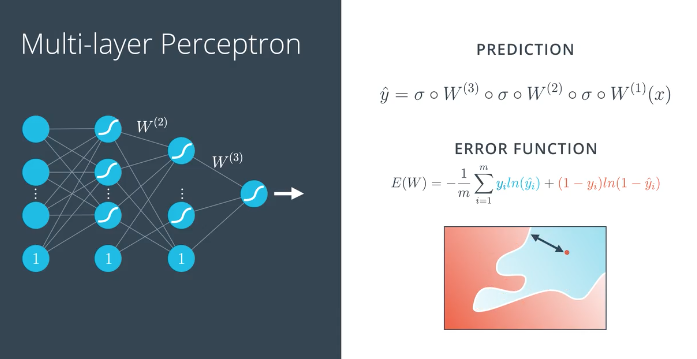
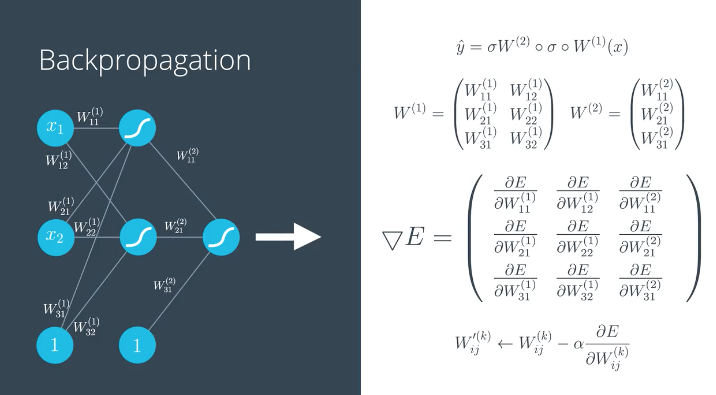
反向传播 (backpropagation function)
神经网络模型训练过程
- 进行前向反馈运算.
- 将模型的输出与期望的输出进行比较.
- 计算误差.
- 向后运行前向反馈运算(反向传播),将误差分散到每个权重上->梯度下降
- 更新权重,并获得更好的模型.
- 继续此流程,直到获得好的模型.
链式法则(Chain Rule)
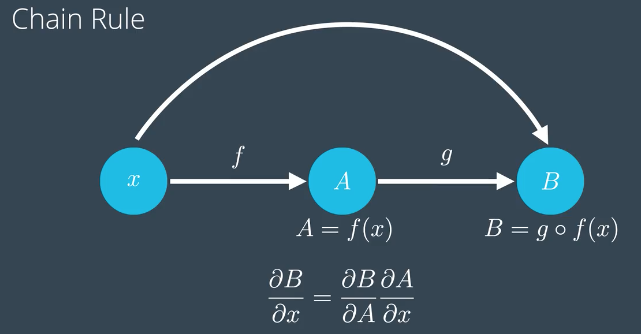

 复合函数的求导,
梯度传递的计算方式
复合函数的求导,
梯度传递的计算方式
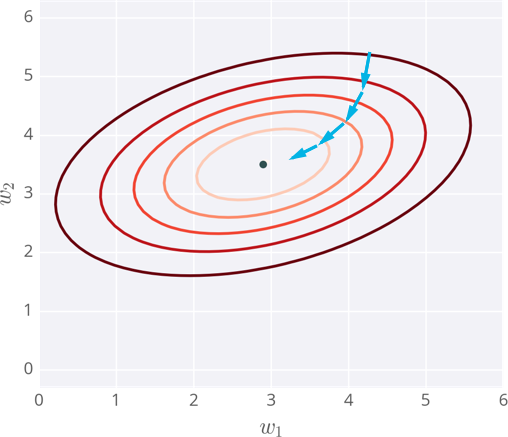
实现梯度下降
画了一个拥有两个输入的神经网络误差示例,相应的,它有两个权重。你可以将其看成一个地形图,同一条线代表相同的误差,较深的线对应较大的误差。
每一步,你计算误差和梯度,然后用它们来决定如何改变权重。重复这个过程直到你最终找到接近误差函数最小值的权重,即中间的黑点。
注意事项
因为权重会走向梯度带它去的位置,它们有可能停留在误差小,但不是最小的地方。这个点被称作局部最低点。如果权重初始值有错,梯度下降可能会使得权重陷入局部最优,例如下图所示。
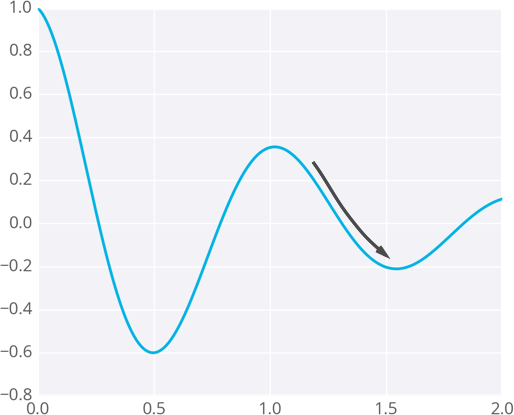 题外话:处于局部最优,就像人生中走到某种境地,以为自己不可能有更高的存在,环顾四周都比自己差;这个时候可以试着重新开始,跳出舒适区,换一个圈子,或许有更好的成就.
题外话:处于局部最优,就像人生中走到某种境地,以为自己不可能有更高的存在,环顾四周都比自己差;这个时候可以试着重新开始,跳出舒适区,换一个圈子,或许有更好的成就.
梯度下降:数学
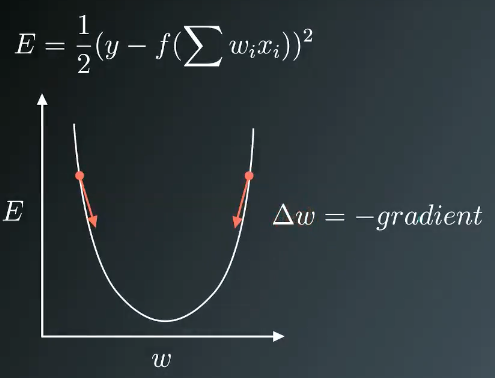 依据数据集的一个数据点xi,可以绘制如上权重w与误差函数的曲线.如果想减小误差E,可以把当前的权重w 减去 gradient(权重的偏导数),来获得比较小的误差E.
依据数据集的一个数据点xi,可以绘制如上权重w与误差函数的曲线.如果想减小误差E,可以把当前的权重w 减去 gradient(权重的偏导数),来获得比较小的误差E.
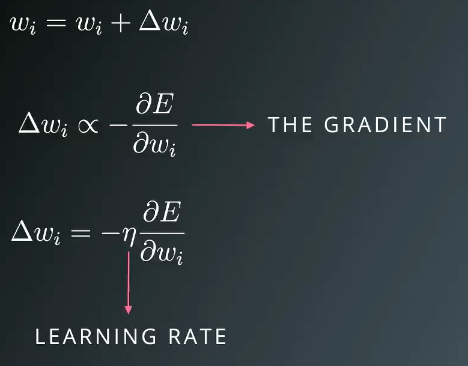
每次按一定比率η(学习率)更新权重
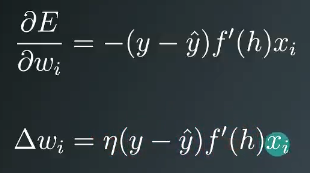

定义一个误差项(Error term)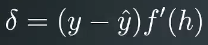
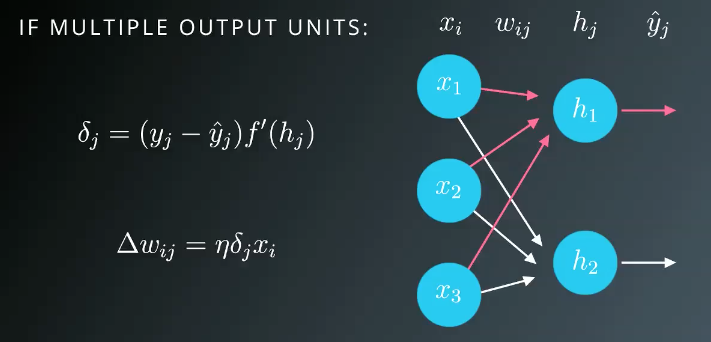
多个输出的时候,权重更新项wij如上图
梯度下降数学推导
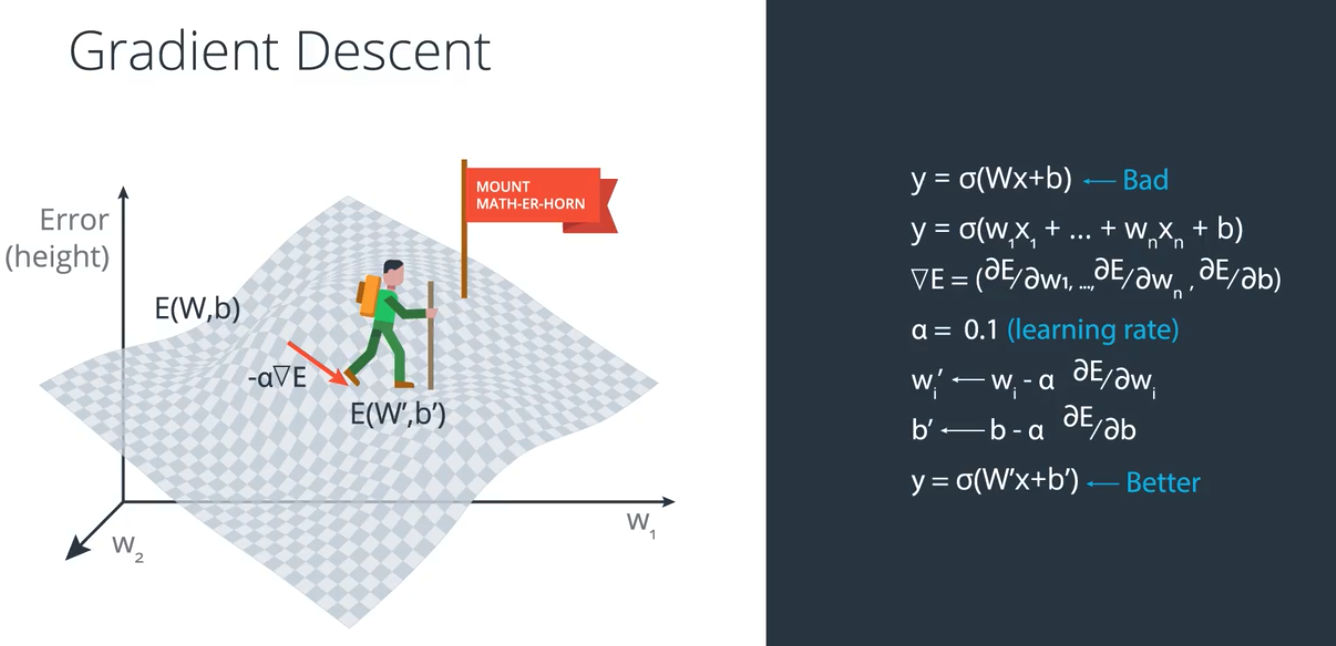 搭建好网络结构之后,会随机初始化权重weight,一开始的结果可能会比较差,误差函数比较大,通过对误差函数进行求导,并按一定比率 α (学习率 learning rate)对权重进行更新,最终,会得到比较好的模型.
搭建好网络结构之后,会随机初始化权重weight,一开始的结果可能会比较差,误差函数比较大,通过对误差函数进行求导,并按一定比率 α (学习率 learning rate)对权重进行更新,最终,会得到比较好的模型.
以sigmoid激活函数为例
sigmoid 型函数的导数
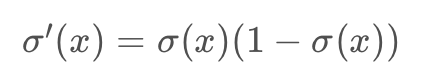


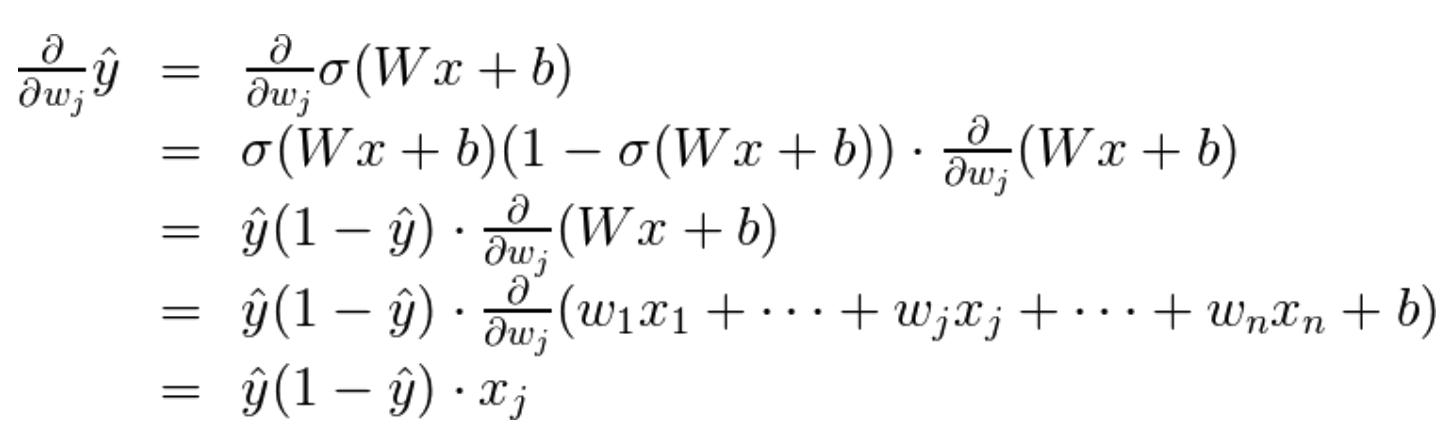
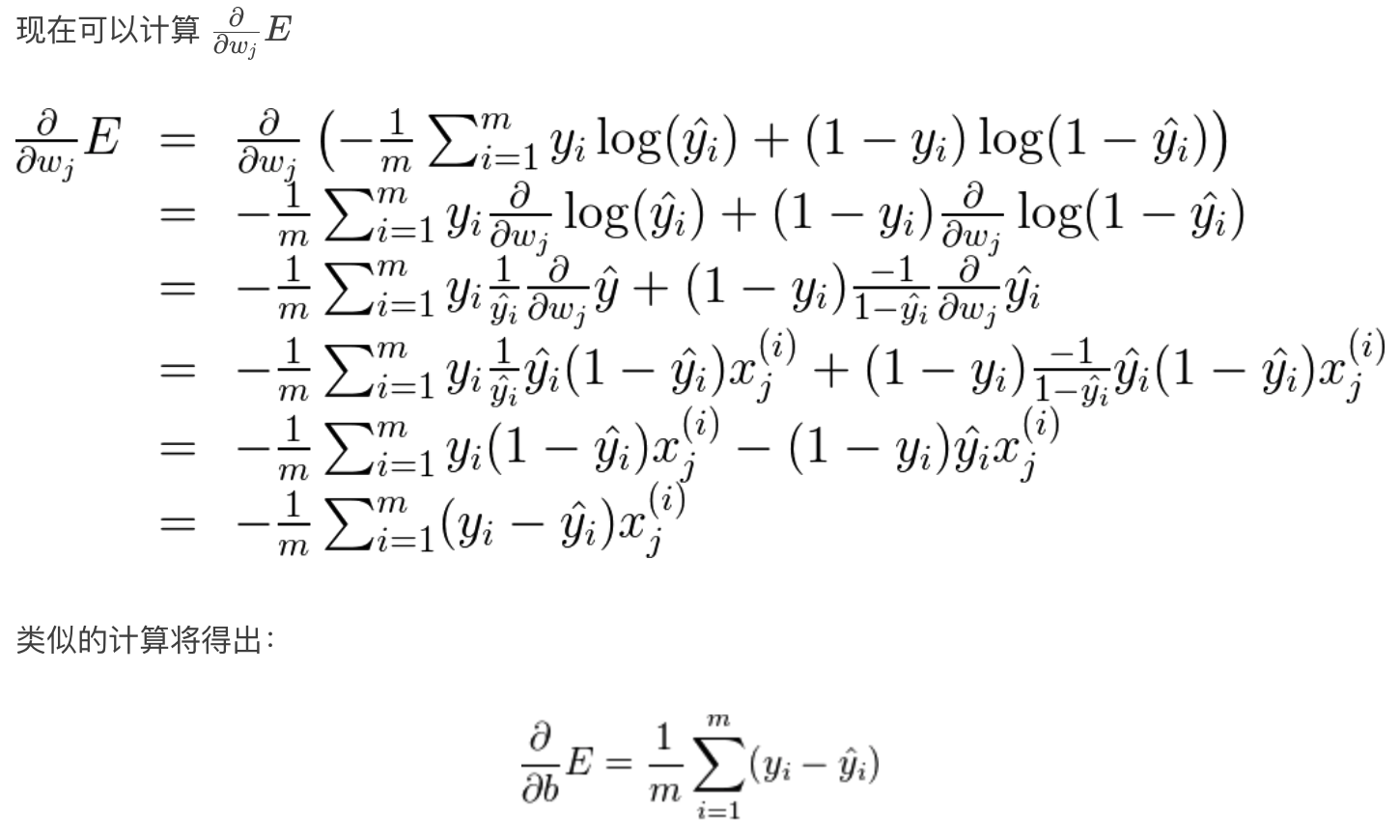
 梯度实际上是标量乘以点的坐标!什么是标量?也就是标签和预测直接的差别。这意味着,如果标签与预测接近(表示点分类正确),该梯度将很小,如果标签与预测差别很大(表示点分类错误),那么此梯度将很大。请记下:小的梯度表示我们将稍微修改下坐标,大的梯度表示我们将大幅度修改坐标。
梯度实际上是标量乘以点的坐标!什么是标量?也就是标签和预测直接的差别。这意味着,如果标签与预测接近(表示点分类正确),该梯度将很小,如果标签与预测差别很大(表示点分类错误),那么此梯度将很大。请记下:小的梯度表示我们将稍微修改下坐标,大的梯度表示我们将大幅度修改坐标。
梯度下降算法
 对每个数据点进行预测,并更新权重,直到error足够小
对每个数据点进行预测,并更新权重,直到error足够小
梯度下降:

# Defining the sigmoid function for activations
# 定义 sigmoid 激活函数
def sigmoid(x):
return 1/(1+np.exp(-x))
# Derivative of the sigmoid function
# 激活函数的导数
def sigmoid_prime(x):
return sigmoid(x) * (1 - sigmoid(x))
# Input data
# 输入数据
x = np.array([0.1, 0.3])
# Target
# 目标
y = 0.2
# Input to output weights
# 输入到输出的权重
weights = np.array([-0.8, 0.5])
# The learning rate, eta in the weight step equation
# 权重更新的学习率
learnrate = 0.5
# the linear combination performed by the node (h in f(h) and f'(h))
# 输入和权重的线性组合
h = x[0]*weights[0] + x[1]*weights[1]
# or h = np.dot(x, weights)
# The neural network output (y-hat)
# 神经网络输出
nn_output = sigmoid(h)
# output error (y - y-hat)
# 输出误差
error = y - nn_output
# output gradient (f'(h))
# 输出梯度
output_grad = sigmoid_prime(h)
# error term (lowercase delta)
error_term = error * output_grad
# Gradient descent step
# 梯度下降一步
del_w = [ learnrate * error_term * x[0],
learnrate * error_term * x[1]]
# or del_w = learnrate * error_term * x
梯度下降算法
 现在我们知道输出层的误差
现在我们知道输出层的误差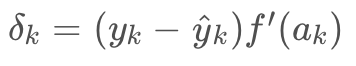 ,隐藏层误差是
,隐藏层误差是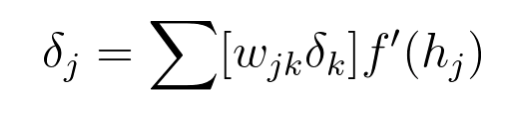
考虑一个简单神经网络,它只有一个隐藏层和一个输出节点.这是通过反向传播更新权重的算法概述:

过拟合和欠拟合(overfitting & underfitting)


早期停止 Early stopping
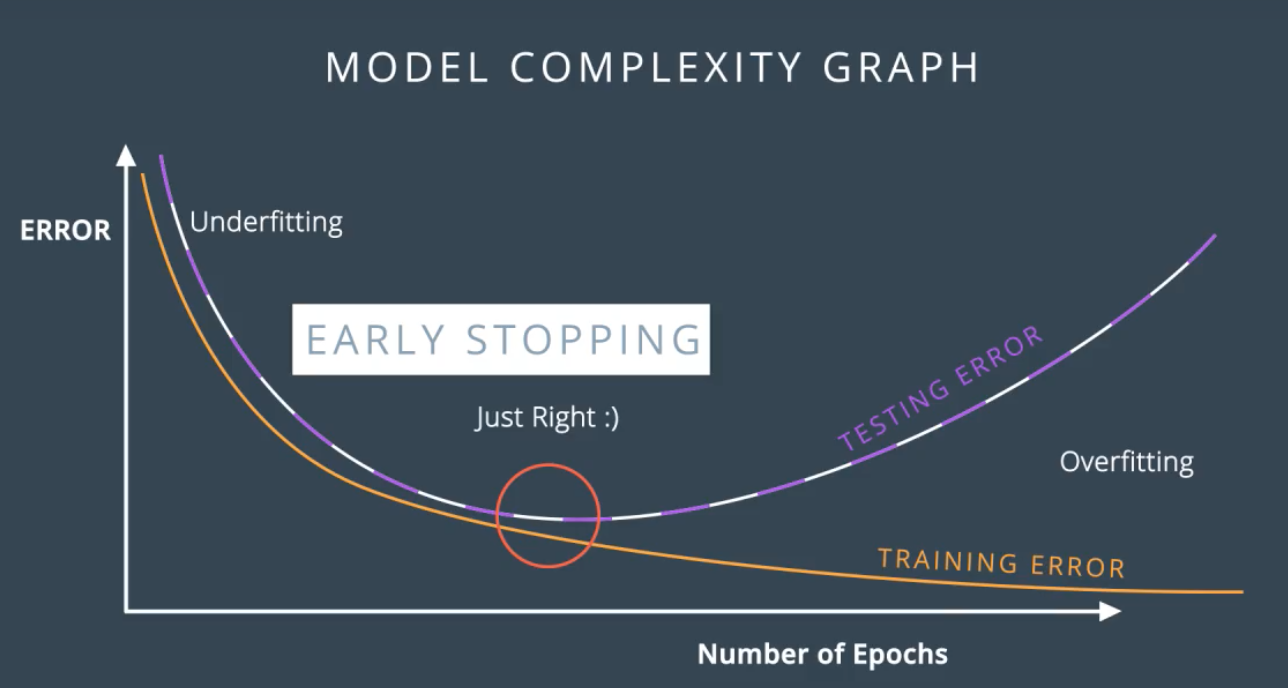 当验证精度挺高之后开始降低,而训练精度依然在不断提高,则可以停止训练.
再继续训练会过拟合,训练精度变高,但是验证精度反倒不高,过拟合时模型泛化能力比较差.
当验证精度挺高之后开始降低,而训练精度依然在不断提高,则可以停止训练.
再继续训练会过拟合,训练精度变高,但是验证精度反倒不高,过拟合时模型泛化能力比较差.
避免过拟合的方法
1.正则化(regularization)
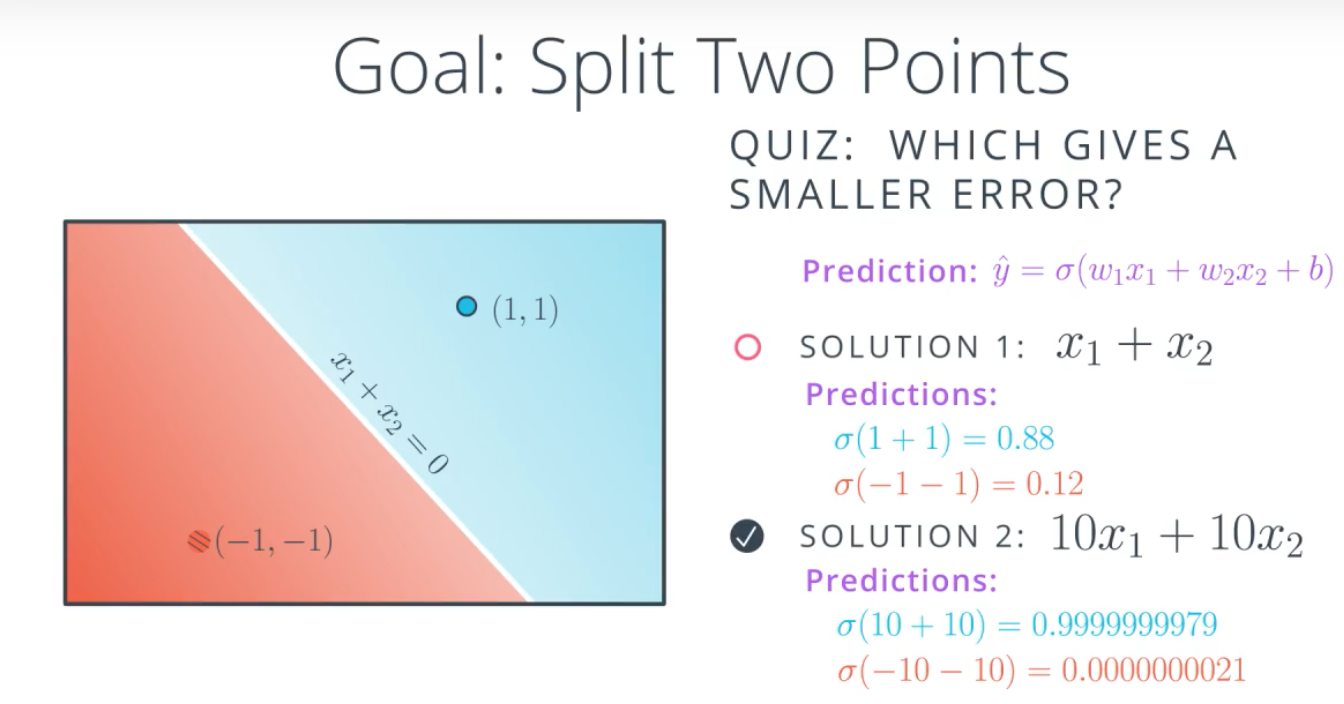
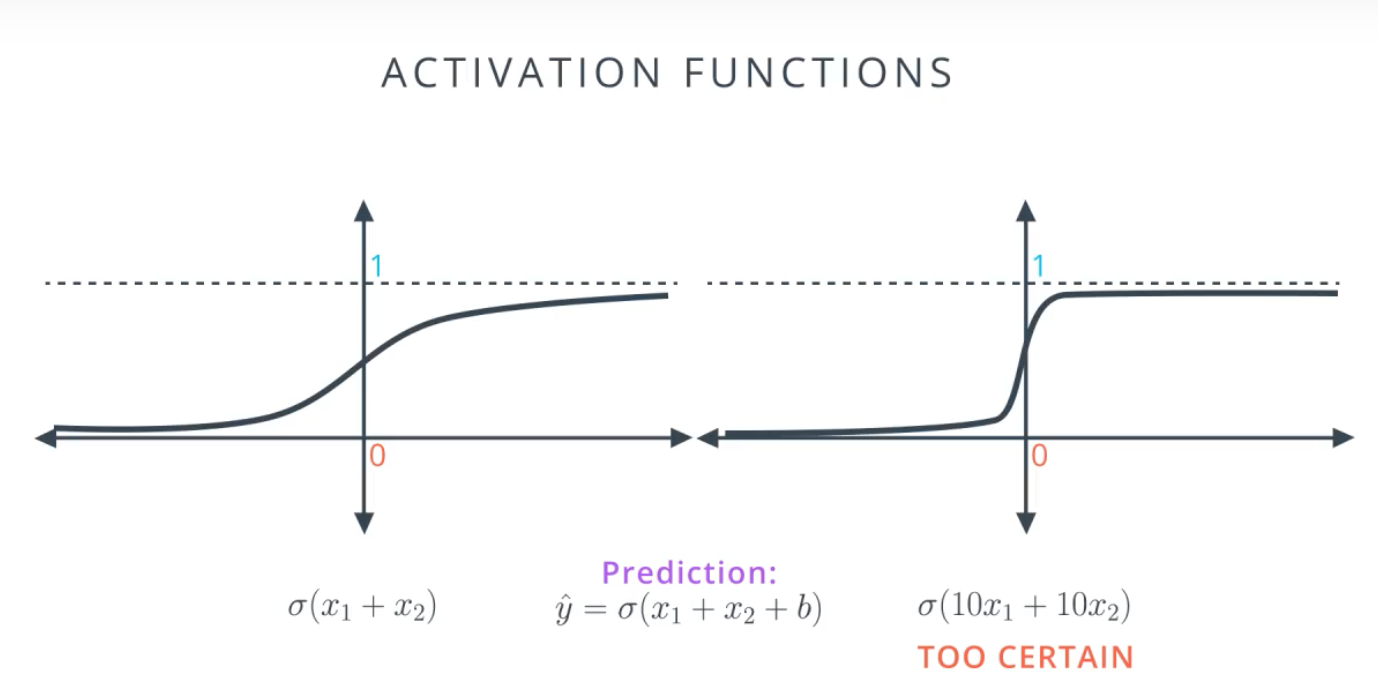 如图,同样比例的权重,如果把权重设置得比较大,那么得到的预测结果两级分化比较严重.weight不宜过大.
如图,同样比例的权重,如果把权重设置得比较大,那么得到的预测结果两级分化比较严重.weight不宜过大.
 人工智能的症结在于坏的模型对预测结果过去确定,好的模型预测结果模棱两可.
人工智能的症结在于坏的模型对预测结果过去确定,好的模型预测结果模棱两可.

 可以通过正则化来调节权重,避免权重过大.
可以通过正则化来调节权重,避免权重过大.
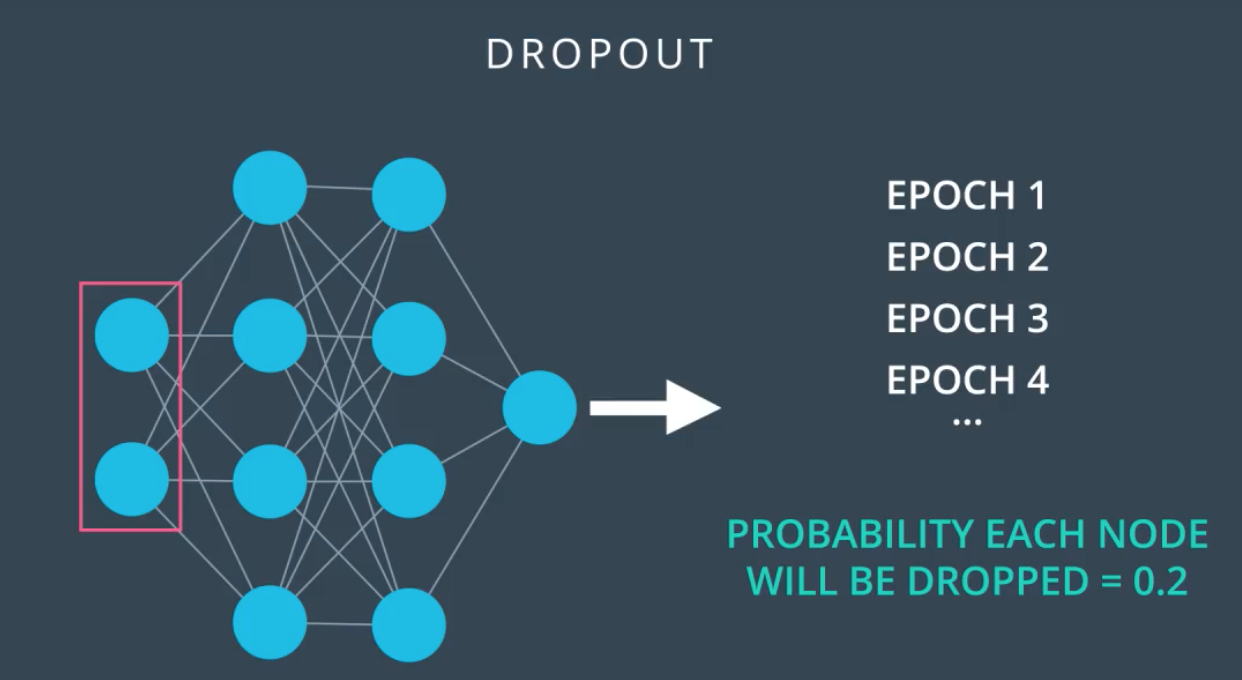
2.Dropout
训练过程中,随机的关闭一定比例的节点,为了其他节点得到更多的训练
局部最低点
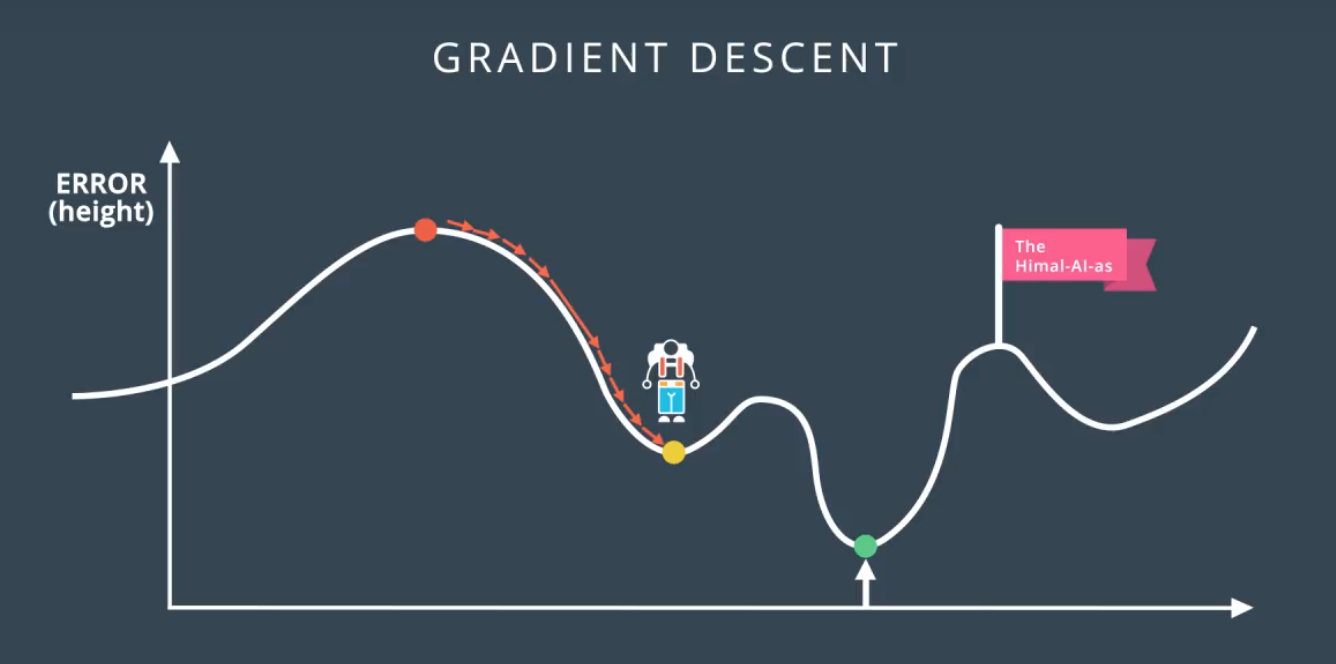
对策:1.随机重新开始

2.动量 Momentum

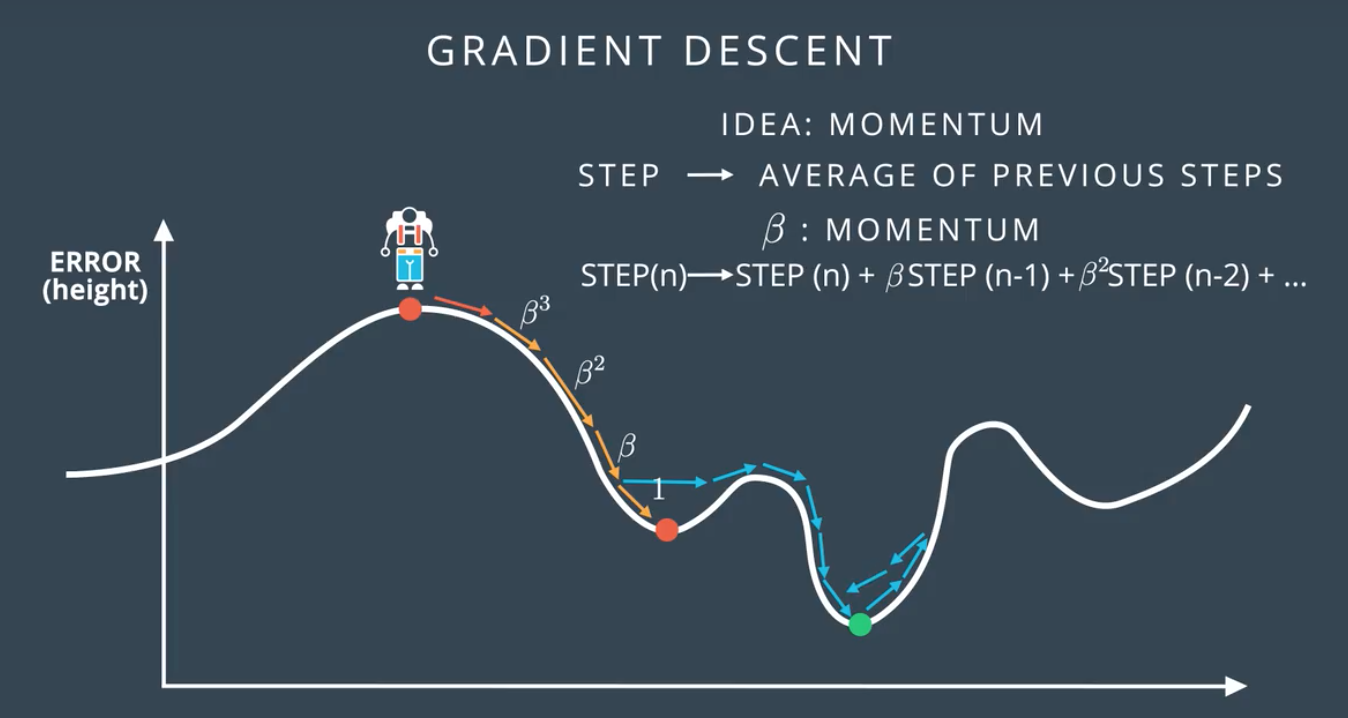 选择比较大的步子,可以越过局部低谷,步子的大小受前面步子大小调节,离得越近,影响越大
选择比较大的步子,可以越过局部低谷,步子的大小受前面步子大小调节,离得越近,影响越大
梯度消失
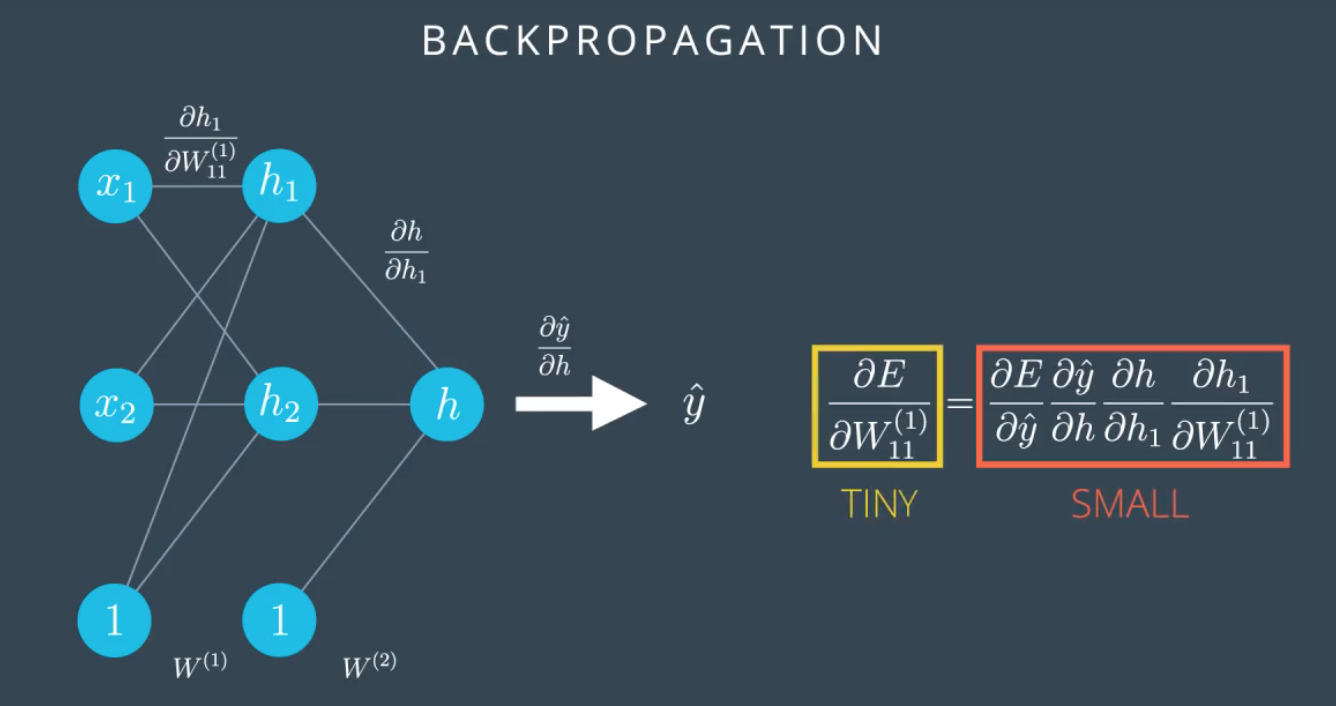 随着网络层级的加深,误差梯度会逐级减小
随着网络层级的加深,误差梯度会逐级减小
其他激活函数
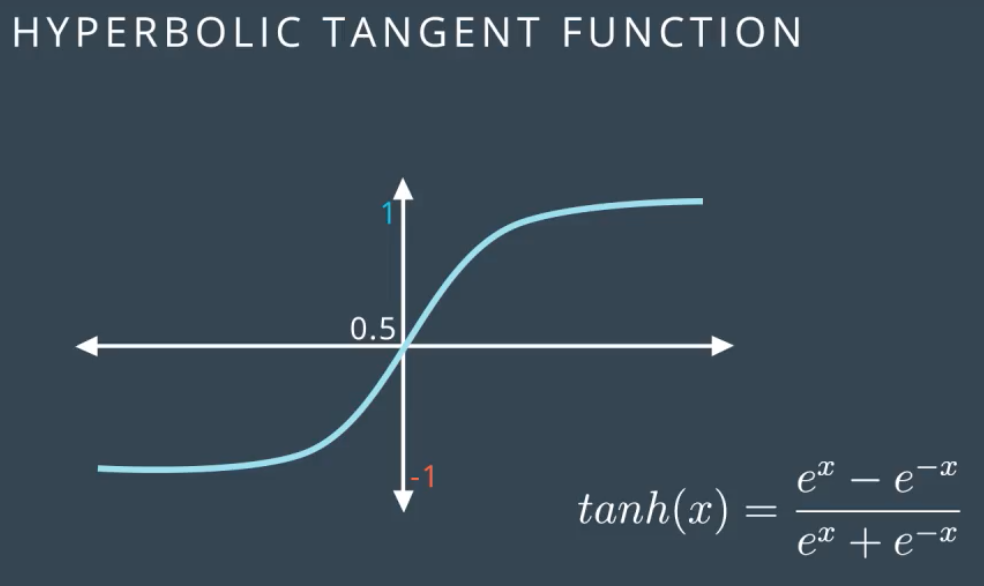
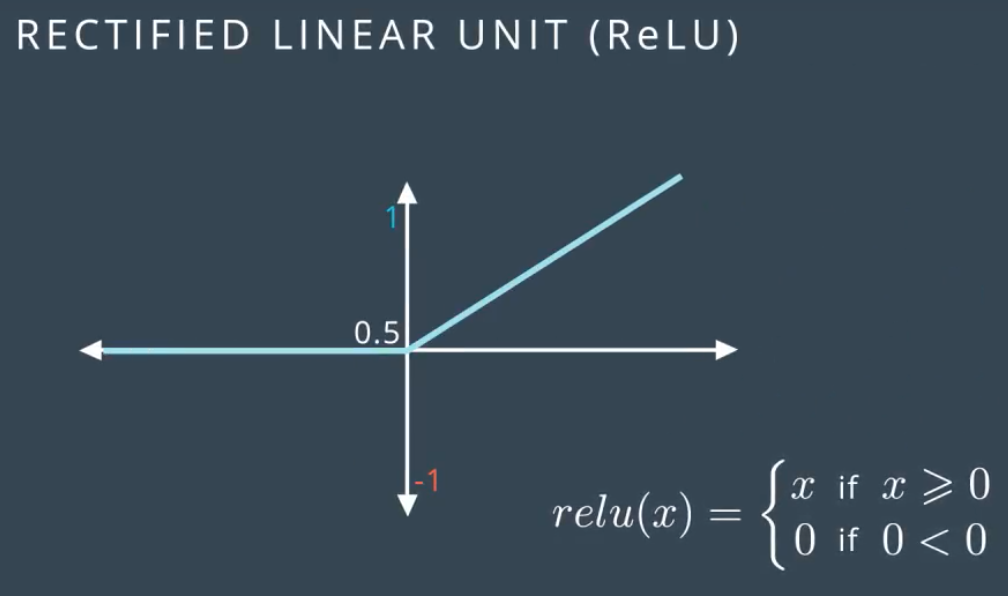
批次和随机梯度下降 batch&stochastic gradient descent
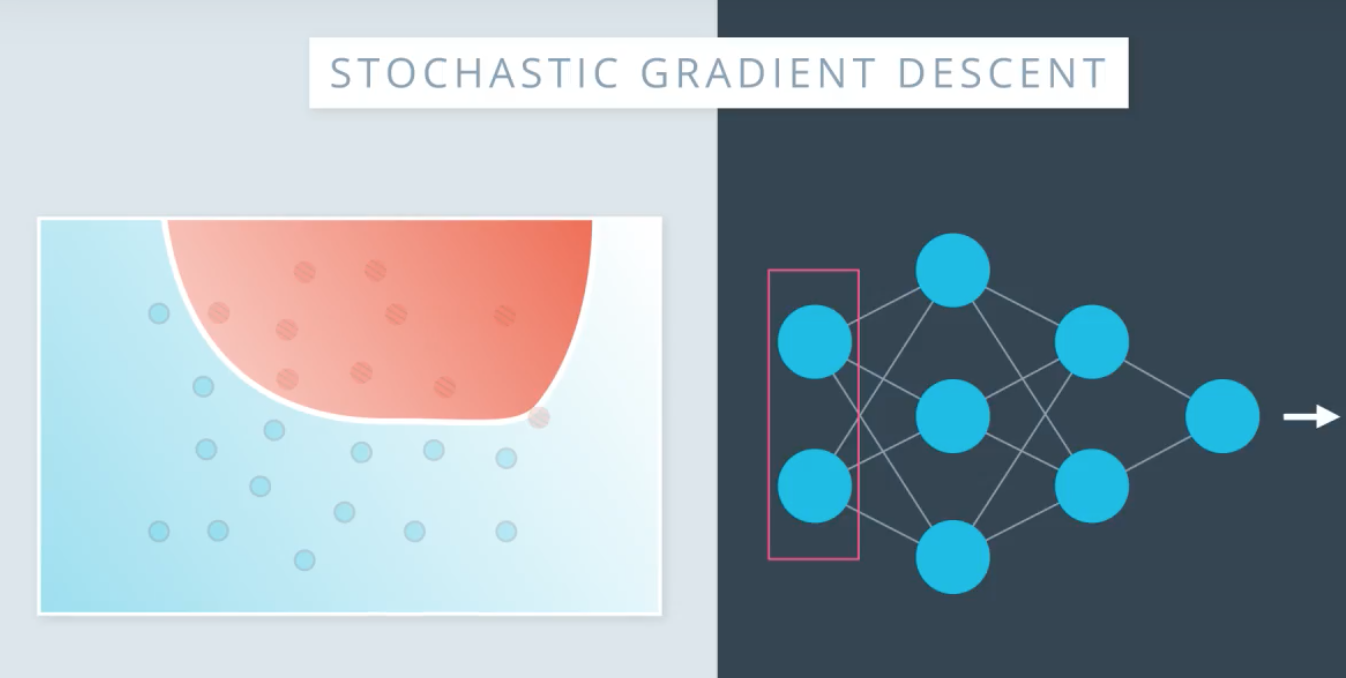 把所有数据集随机拆包,一次只用其中的一个数据集进行训练,在相同运算量的情况下可以多次更新权重,达到比较的训练效果
把所有数据集随机拆包,一次只用其中的一个数据集进行训练,在相同运算量的情况下可以多次更新权重,达到比较的训练效果
学习速率衰退
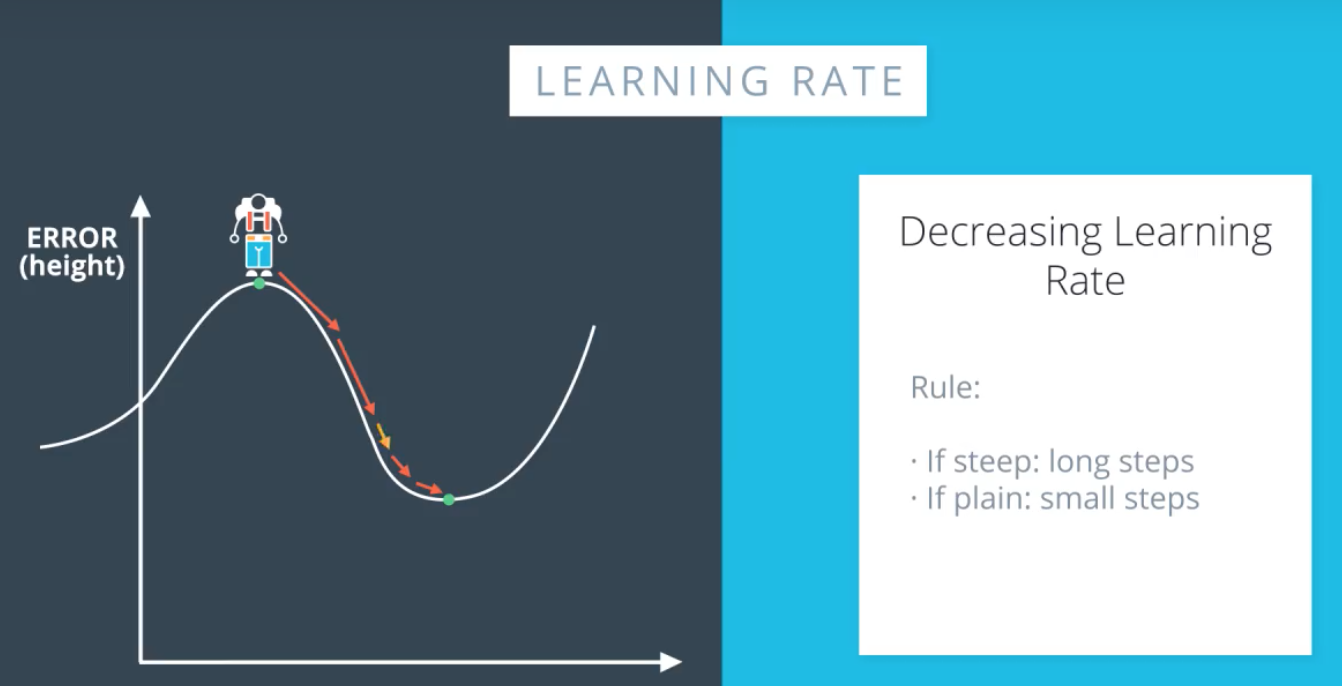 梯度大的地方,step大,梯度大的地方,step小.
梯度大的地方,step大,梯度大的地方,step小.