前置概念
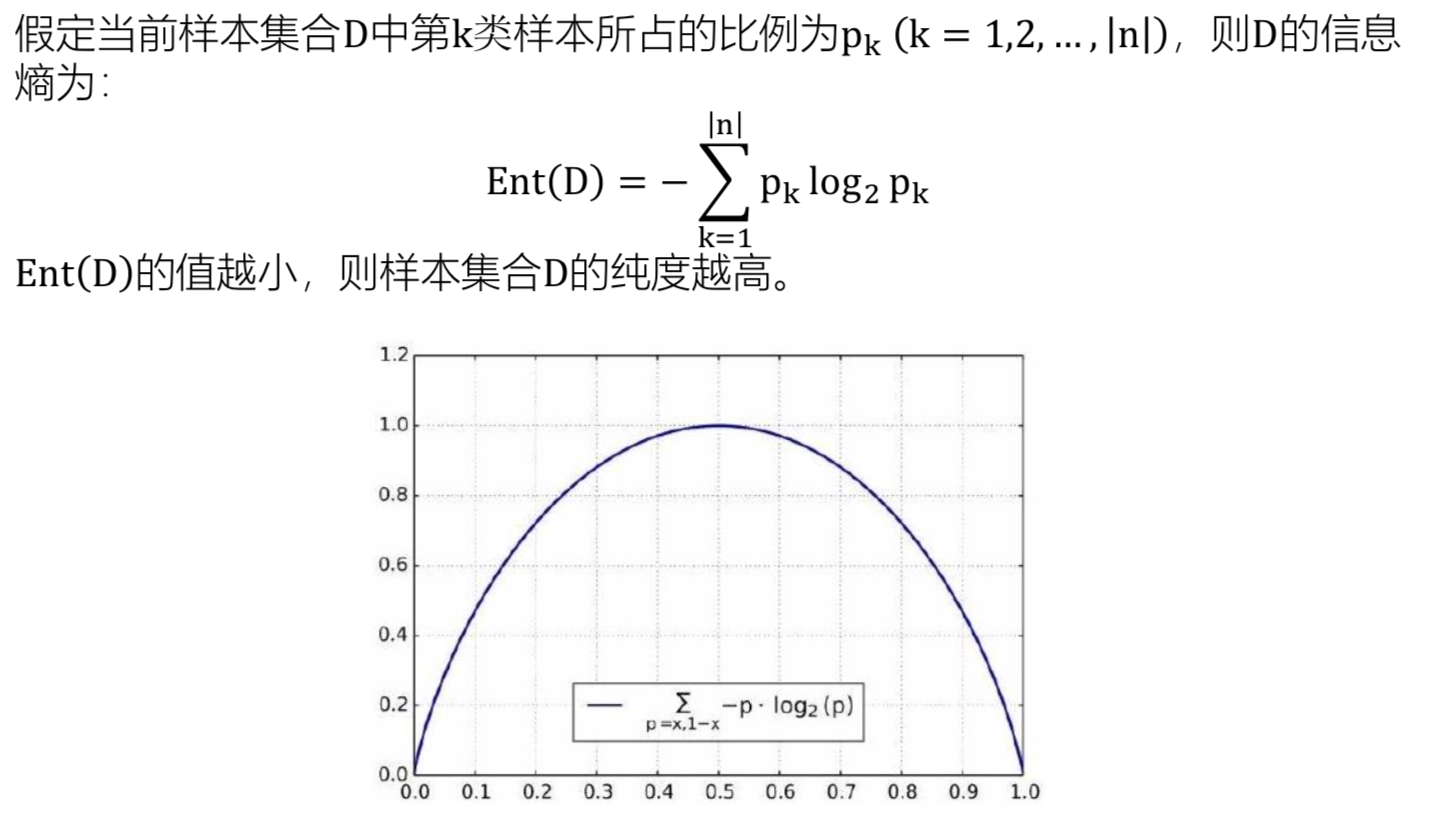
- Entropy(墒): 热力学中表征无知状态的参量之一, 其物理意义是体系混乱程度的度量.
- Information Entropy(信息墒):信息墒是用来消除随机不确定性的东西，度量样本集合纯度的指标
树模型 & 线性模型
- 线性模型
对每个特征进行加权求和
score = f(Wx1X1 + Wx2X2 + Wx3X3 + …) - 树模型
根据每个特征值, 对样本进行分类
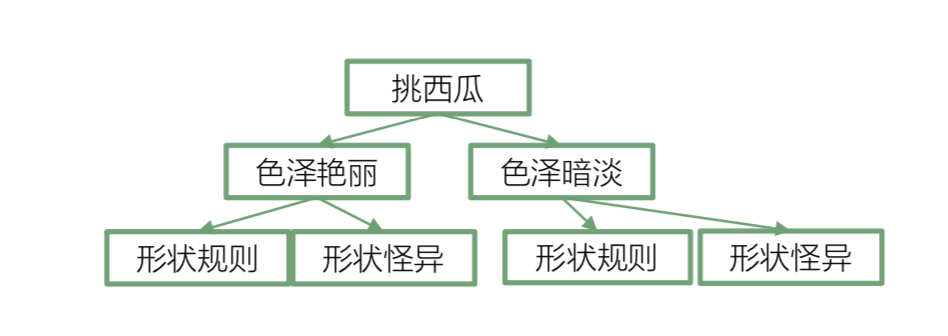
决策树
可以用决策树对数据进行分类, 可以用 信息纯度 来衡量分类效果好坏.
* 目标: 分类后 每个页节点的数据都是同一类别(纯度越高越好)
* 衡量分类效果好坏的指标:
- ID3: 信息增益
- C4.5: 信息增益率
- CART: 基尼系数
ID3: 信息增益
信息增益越大,分类效果越好
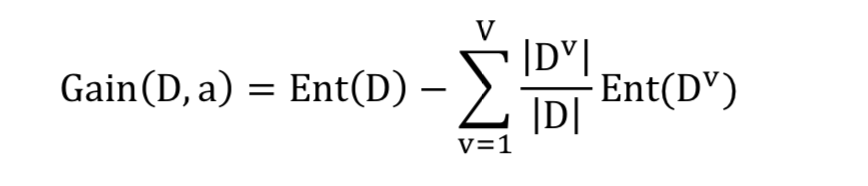a 代表某一属性, Dv 是属性a中一个类别的数量.比如属性a是西瓜的 色泽, 那Dv可以是色泽为 乌黑 的西瓜的数量.
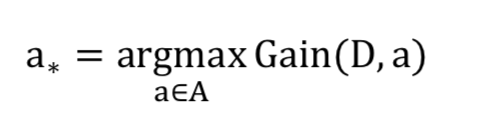使用这个标准存在一个问题, 属性对目标数据的分类越细,越有优势. 举一个极端的例子, 如果用数据的编号对数据进行分类. 那么每一条数据都是一个类别, 是把每个类别都分出来了, 但是并没有实际意义
C4.5: 信息增益率
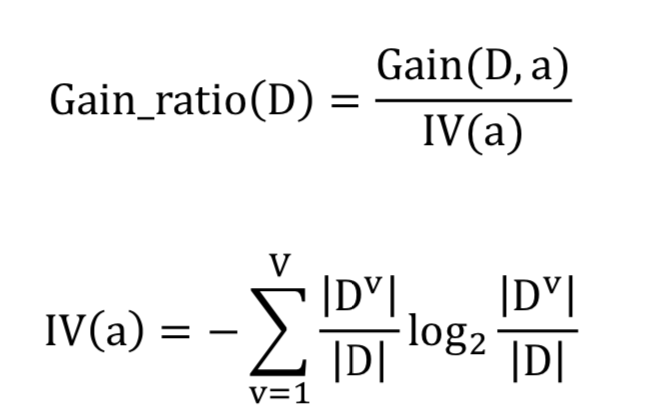IV(a)是属性固有的值, 类别越多,IV(a)越大
比如一个属性只有两类 IV(a) = -1/2 * log2(1/2) * 2 = 1
另一个属性有四个类别 IV(a) = -1/4 * log2(1/4) * 4 = 2
通过把信息增益除以对应属性的IV值对类比较多的属性给以一定的惩罚, 可以获得比较合理的纯度指标
但是增益率对类别少的属性有偏好, 不会直接选择增益高的属性
那么能不能先选择增益高的属性, 然后再从增益高的属性里边选择增益率高的属性?
CART: 基尼系数
从样本中随意抽取两个样本, 它们为不同类别的概率.
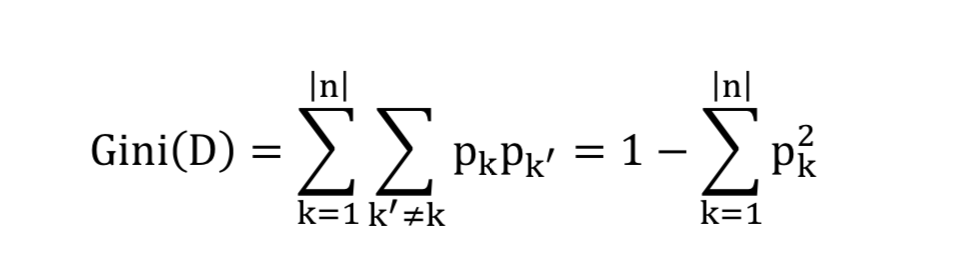基尼系数越小, 样本纯度越高
针对属性a的基尼系数为:
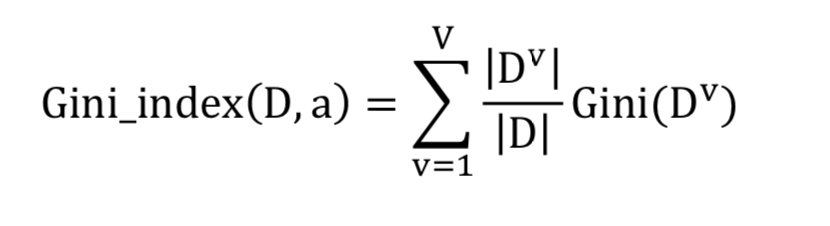
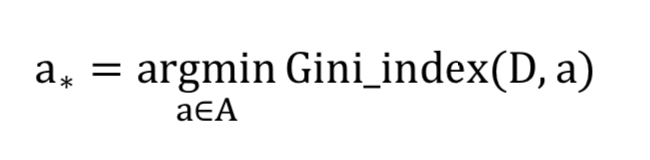每次选取属性来对数据进行分类时选择基尼系数最小的.
缺失值的处理
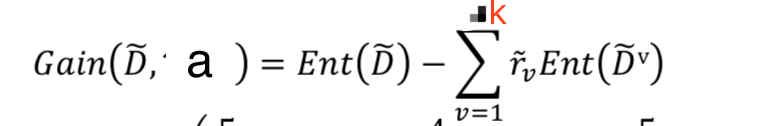
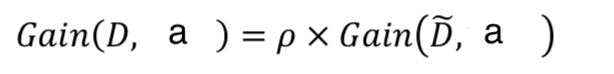计算有缺失值的属性的信息增益时, 先忽略有缺失值的那部分数据, 按照没有缺失值的方式去计算,最后把计算结果乘以缺失的比例 p, 就得到有缺失值的属性的信息增益, 即缺失值越多, 这个属性被用来做分类依据的可能性越低.
连续值的处理
选择分区的时候, 可以使用二分法, 从中间开始分割数据, 每次根据结果,选择往左边二分,还是往右边二分.
过拟合
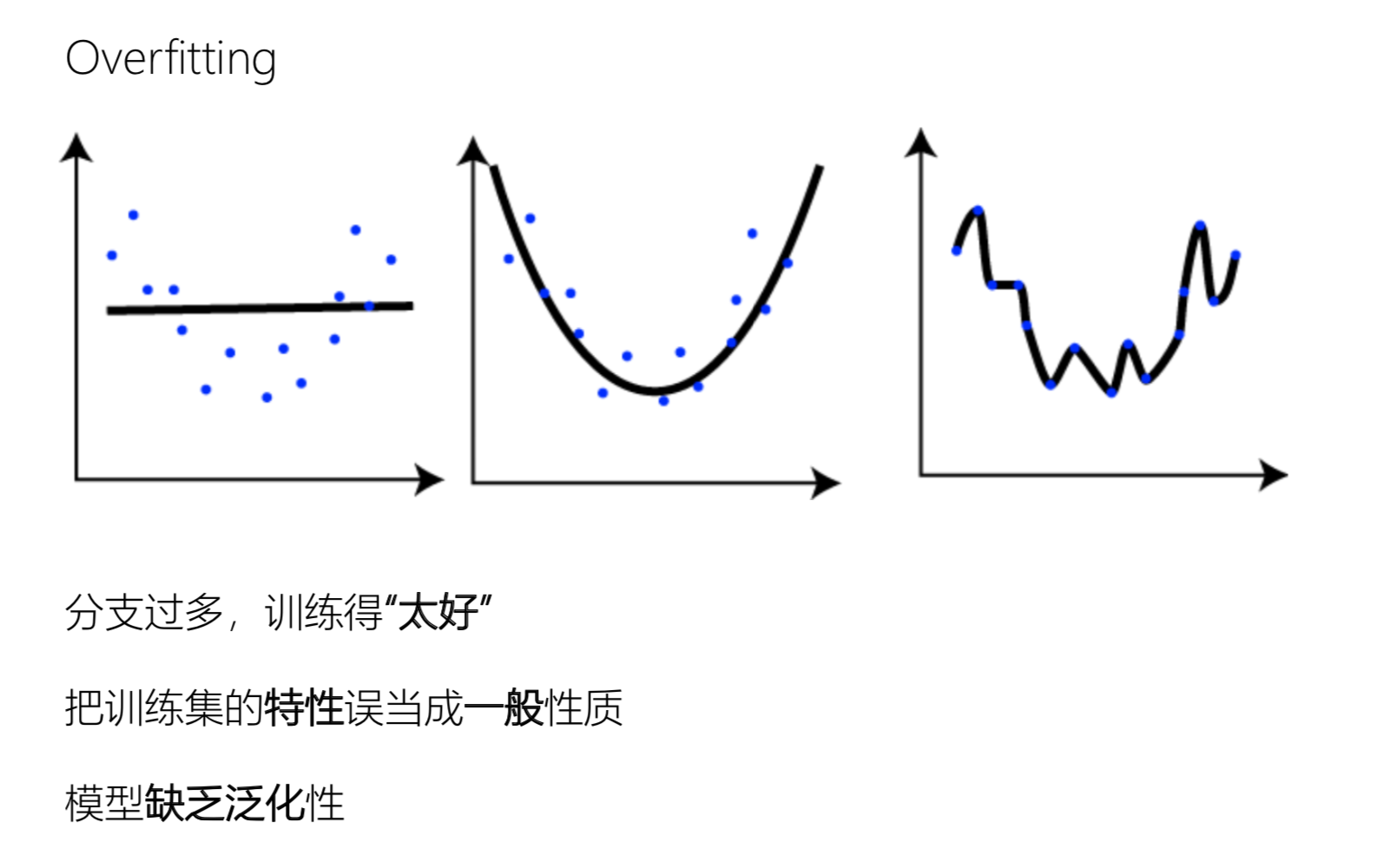
如果没有进行处理，决策树会遍历每个属性，在每个属性上建立分支，以最大化减小信息墒，这样子容易过拟合。
** 可以通过如下方式，防止过拟合：
- 预剪支
每次进行进行分支之前，根据一个指标，可以是信息墒降低的值，或者是精度提升的程度，来决定是进行分支，还是保留当前的页节点
- 后剪支
按照贪婪的方式，对所有属性进行分支处理，最后再自下而上，判断合并分支之后，精度或墒是否达到一定阀值。
Tips
- 数据量和特征数应该保持一定比例， 如果只有少量的数据而有过多的数据，容易出现过拟合
- 可以使用PCA对数据绛纬,减少特征数,防止过拟合
- 减少深度, 设置max_depth
- 设置合适的页节点数量, min_samples_split
- 训练前把数调整平衡, 防止数倾向与那些优势权重 * …
随机森林
集成学习(Ensemble learning)
集成学习通过构建并结合多个学习器来完成学习任务.只包 含同种类型的个体学习器，这样的集成是“同质”的;包含不 同类型的个体学习器，这样的集成是“异质”的. 集成学习通 过将多个学习器进行结合，常可获得比单一学习器显著优 越的泛化性能.
RandomForest-Bagging
- 随机有放回的从样本中抽取少量数据.
- 随机选取一定量的属性作为决策树的分类依据.
- 同时训练大量的决策树，最后的预测结果通过投票决定.
** 优点：泛化能力强， 不容易过拟合；对缺失值不敏感； 不需要对高维数据做特征选择；容易进行并行化计算
** 缺点：取值划分比较多的属性有优势
Boosting-GDBT(Gradient Boosting Decision Tree)
Boosting，集成学习方法之一. 一种用来提高弱分类算法准确度的方法，属于迭代算法. 通过不断地使用一个弱学习器 弥补 前一个弱学习器的“不足”的过程， 来 串行 地构造一个较强的学习器，能够使目标函数值足够小.
构建过程:
- 先用一个初始值来学习一棵决策树(一个主要特征, 做粗略的预测)
- 叶子处可以得到预测的值，以及预测之后的残差(个体的差异, 会造成残差)
- 然后后面的决策树就要基于前面决策树的残差来学习
- 直到预测值和真实值的残差为零(都是同一类别)
- 最后对于测试样本的预测值，就是前面许多棵决策树 预测值的累加
** 一个生活中的例子, 比如预测人的身高
- 首先通过 性别来预测, 男的 172cm, 女的 162cm.
- 通过地区, 北方人+3cm, 南方人-3cm.
- 还其他特征, 依次类推
把所有可以用到的信息都用来预测, 不同特征会在不同程度影响预测值的大小
key words
RF out of bag data包外错误, 随机森林的算法每次会随机从数据中取样本进行训练, 被取的样本之外的数据就是包外数据, 可以通过评估决策树模型在包外数据上的表现来评估单棵决策树训练的好坏.
bootstrap在数据中有放回的随机抽取数据
GBDT AdaBoost XGboost一个提供算法 梯度下降 的 framework