数据结构

02 Jul 2019

时间复杂度

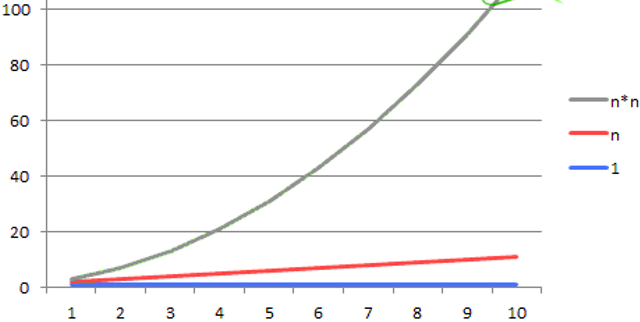
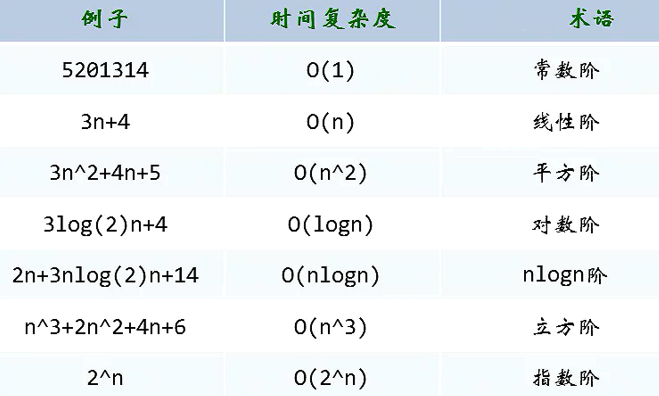
定义：在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度，也就是算法的时间量度，记作：T(n)= O(f(n))。它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。其中f(n)是问题规模n的某个函数。

用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。

一个程序内部执行（循环）的次数

O(1), O(n), O(n*n)对应的曲线

空间复杂度

定义：算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度的计算公式记作：S(n)=O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。

很多时候，可以用空间换时间，通过存储常量来减少运算量

数组 & 链表

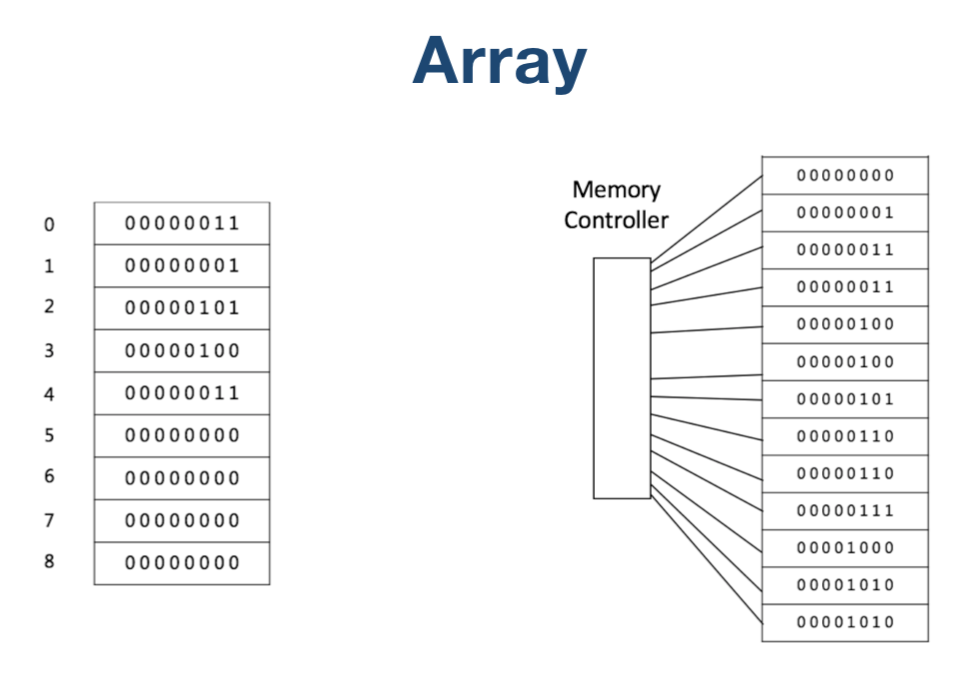
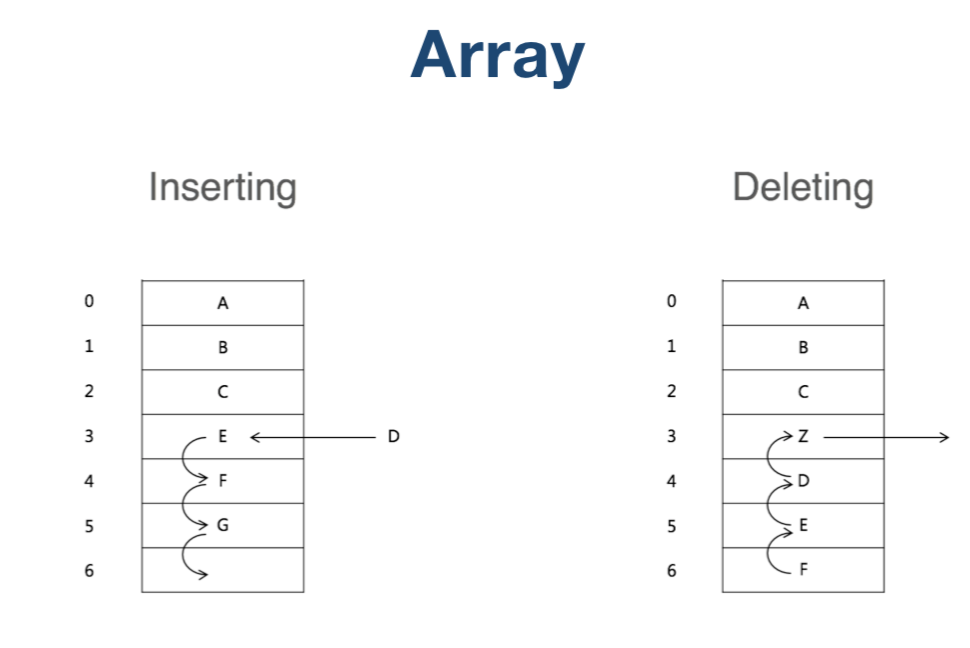
数组：在内存中分配一块连续的空间 添加和删除都需要移动关联的一系列数据

时间复杂度

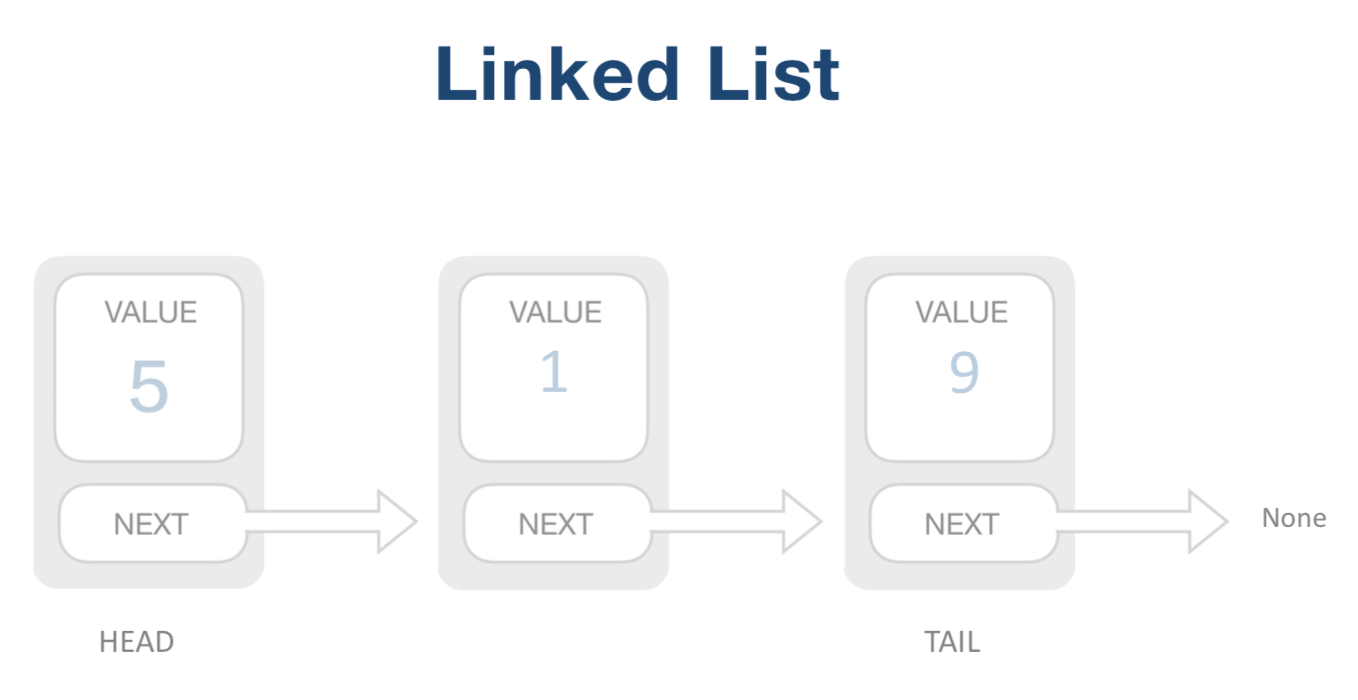
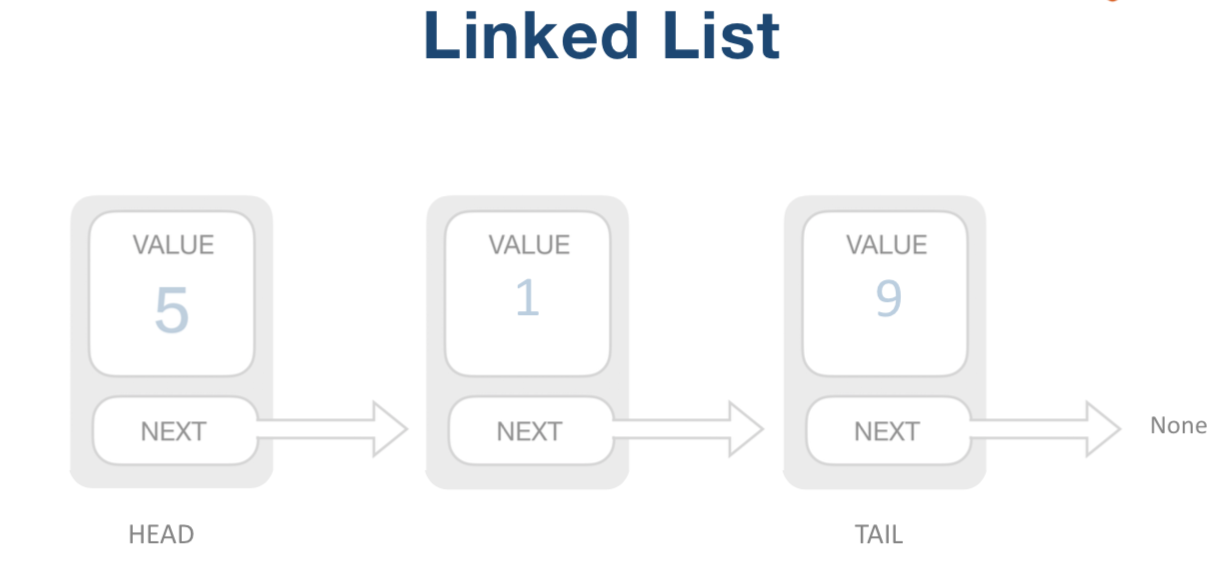
链表：链表中元素不需要存在同一个地方，通过Next指到下一个元素，相对比较灵活 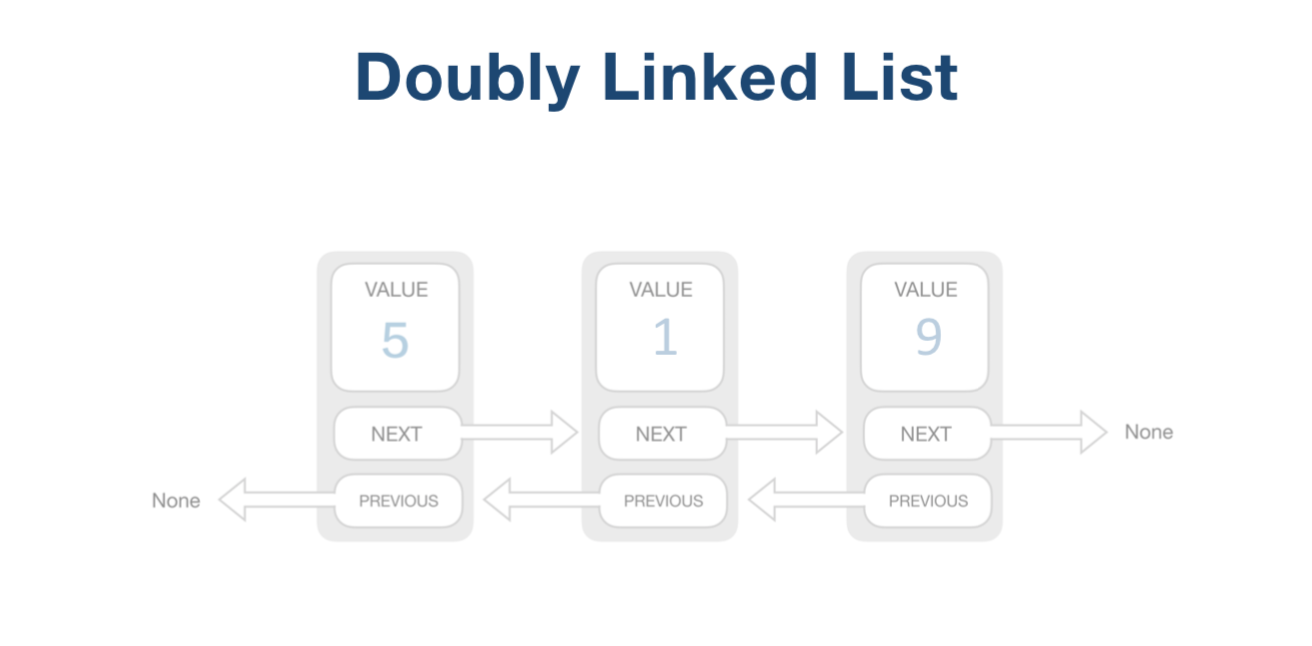插入和移除元素，只需要改两个元素的next指针即可

时间复杂度

Stack & Queue - 栈&队列

Stack

后进先出

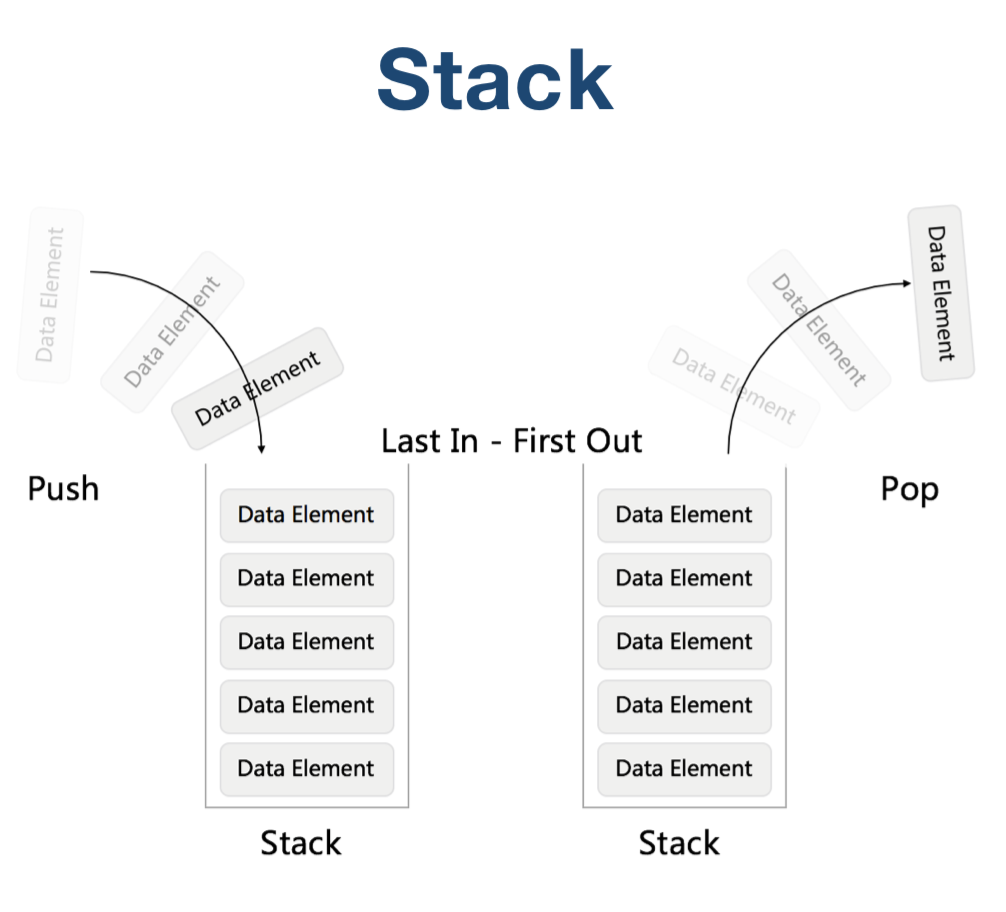
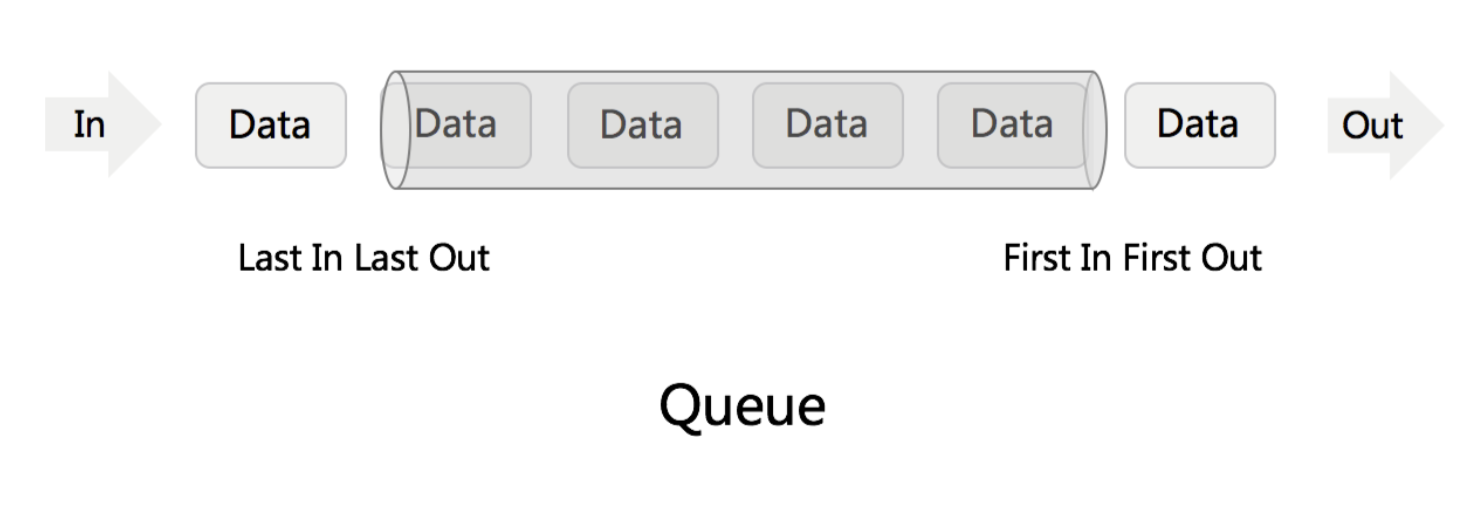
Queue

先进先出

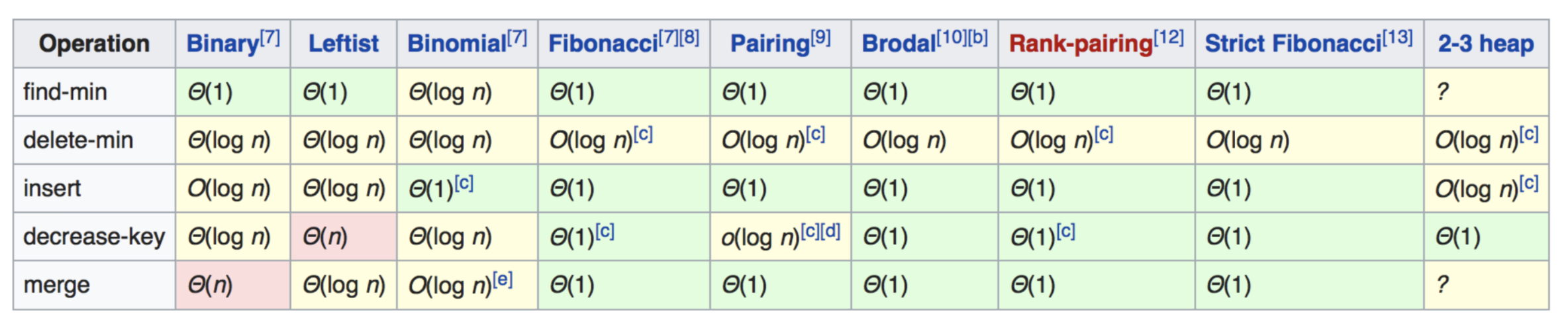
常用数据结构的 复杂度

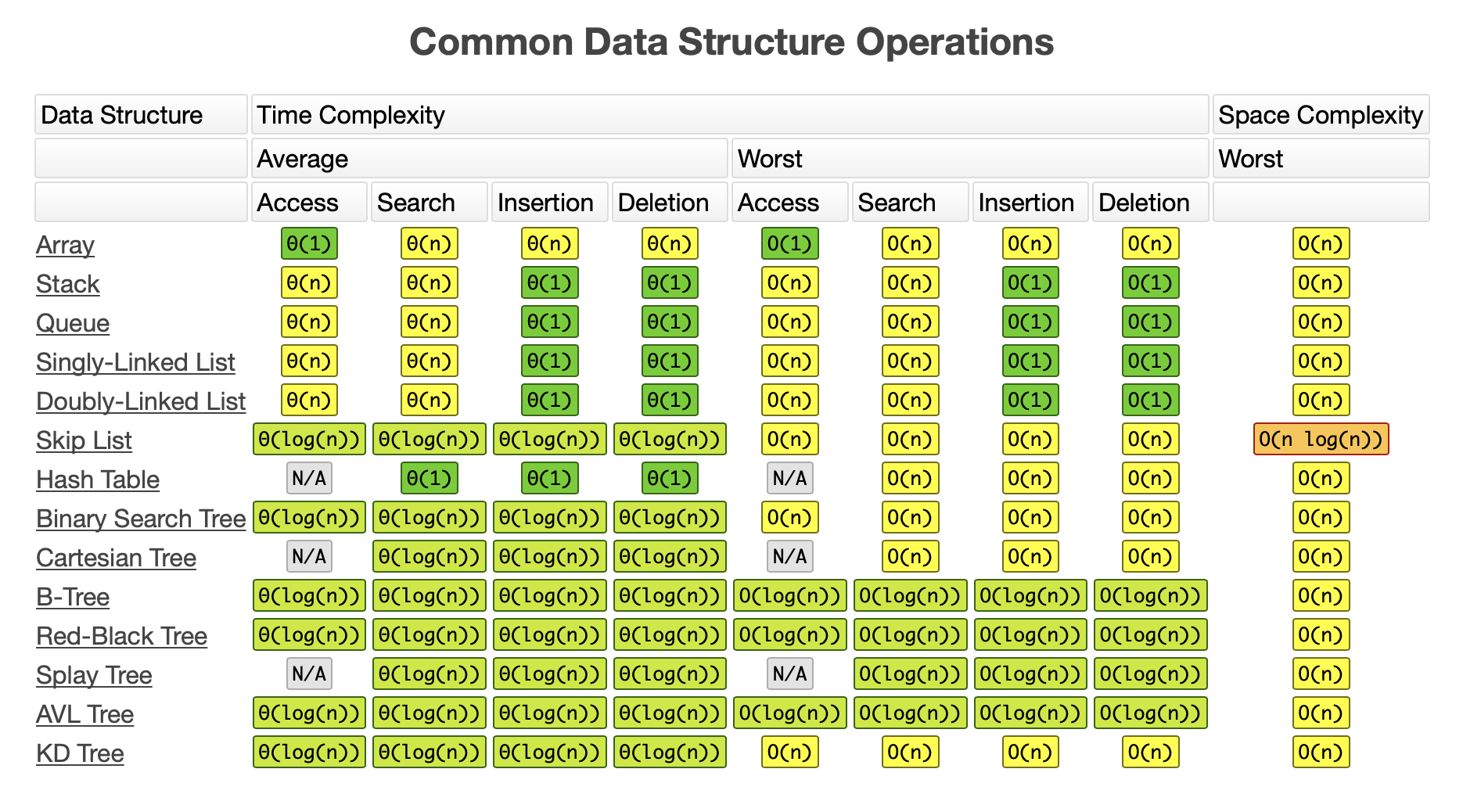
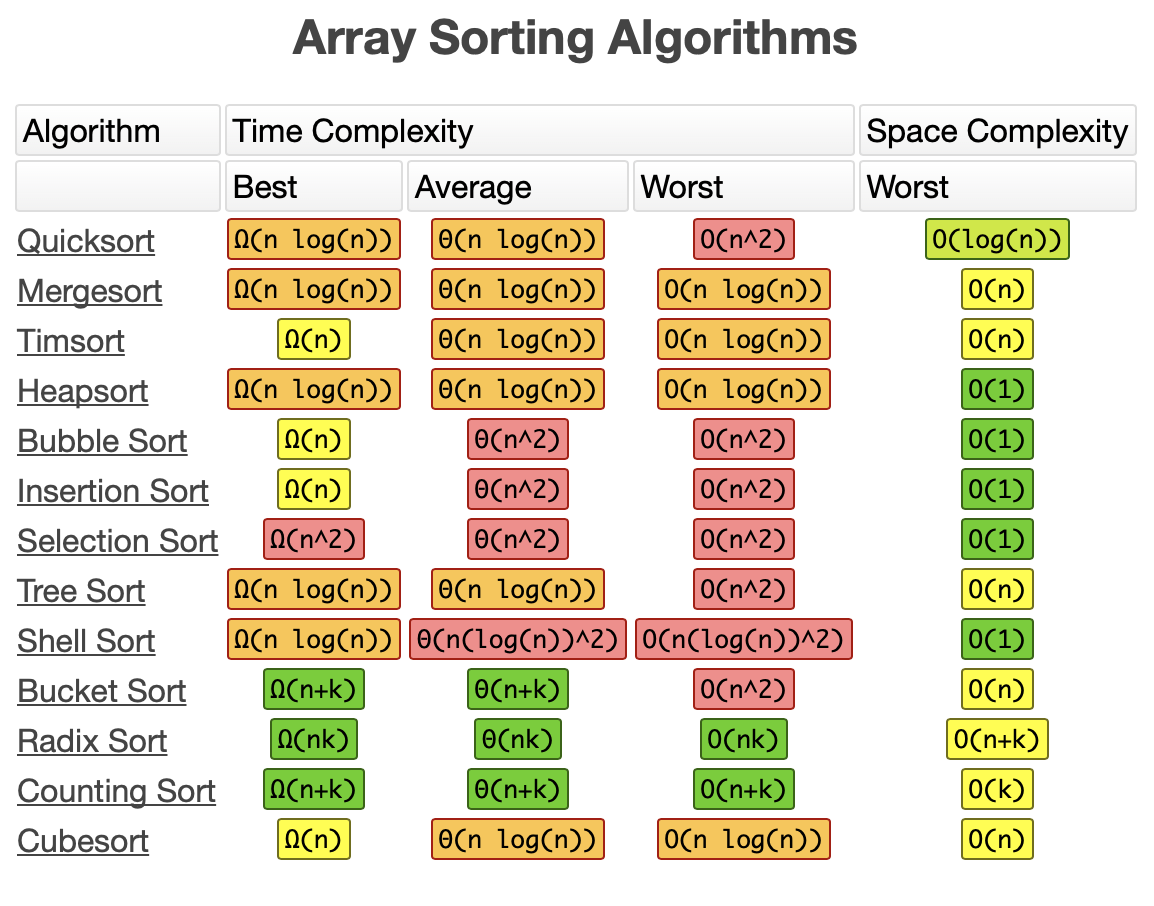
使用例子

/**
 Given a string containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

An input string is valid if:

Open brackets must be closed by the same type of brackets.
Open brackets must be closed in the correct order.
Note that an empty string is also considered valid.
 */

#include <iostream>
#include <string>
#include <stack>
#include <vector>
#include <map>
using namespace std;

class Solution {
public:
    bool isValid(string s) {

        // 1. iterate all elements
        // 2. find all "(" "{" "[", and record
        // 3. get the other parts ")", "]", "}", remove the left one, else return false
        // 4. till the end, if nonthing left, return true, else return false
        stack<char> cached;
        map<char, char> parenthesis;
        parenthesis.insert(pair<char, char>('(', ')'));
        parenthesis.insert(pair<char, char>('{', '}'));
        parenthesis.insert(pair<char, char>('[', ']'));

        for(string::iterator it=s.begin(); it!=s.end(); it++){

            if (parenthesis.count(*it))
            {
                cached.push(*it);
            } else if (!cached.empty() && parenthesis[cached.top()] == *it)
            {
                cached.pop();

            } else{
                return false;
            }
        }

        return cached.empty();
    }
};

int main(){
    vector<string> testStrs{"()", "()[]{}", "(]", "([)]", "{[]}", "]", "", "("};
    for(int i=0; i < testStrs.size(); i++)
    {
        bool isValid = Solution().isValid(testStrs[i]);
        cout << isValid << " ";
    }
    return 0;
}

PriorityQueue - 优先队列

正常进、按照优先级出

常用实现方式

  1. Heap(Binary, Binomial, Fibonacci)
  2. Binary Search Tree

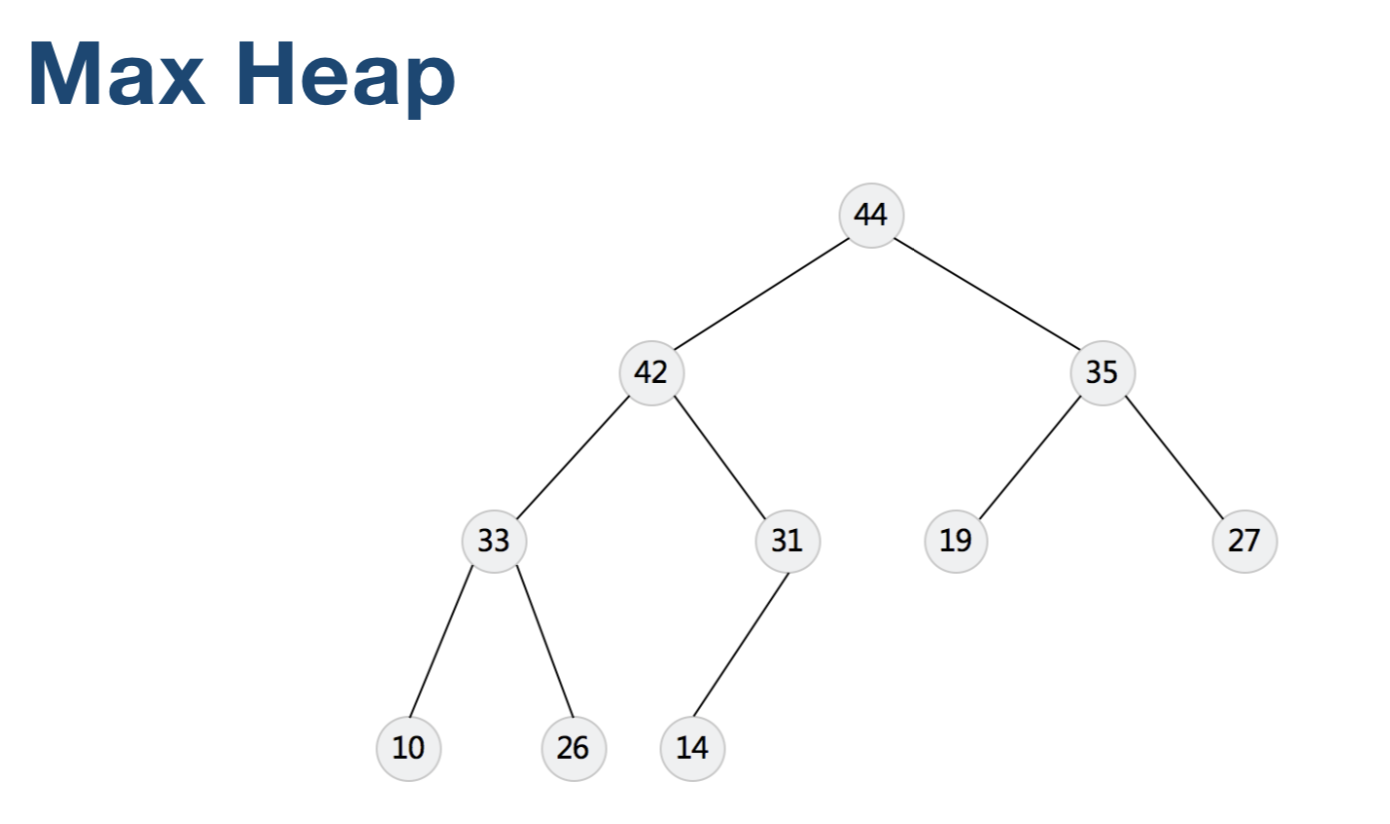
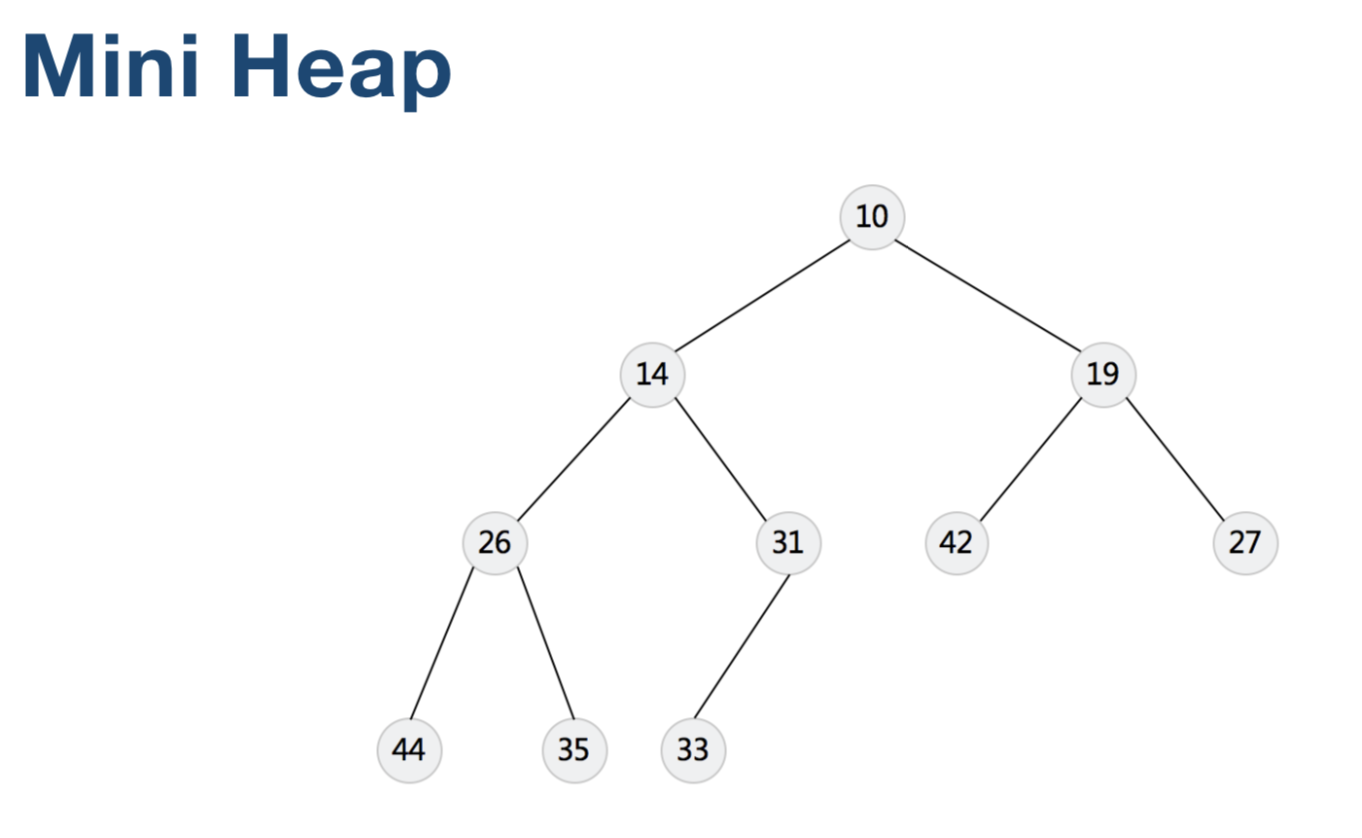
使用例子

/**
 * Your KthLargest object will be instantiated and called as such:
 * KthLargest* obj = new KthLargest(k, nums);
 * int param_1 = obj->add(val);
 * Note:
 * You may assume that nums' length ≥ k-1 and k ≥ 1.
 */

/*
 * int k = 3;
 * int[] arr = [4,5,8,2];
 * KthLargest kthLargest = new KthLargest(3, arr);
 * kthLargest.add(3);   // returns 4
 * kthLargest.add(5);   // returns 5
 * kthLargest.add(10);  // returns 5
 * kthLargest.add(9);   // returns 8
 * kthLargest.add(4);   // returns 8
 * */

// with min priority queue
class KthLargest {
    int _k;
    priority_queue<int, vector<int>, greater<int>> pq{};
public:
    KthLargest(int k, vector<int>& nums) {
        /**
         * create a qp with size k
         * 1. make the first pq
         * 2. run through the whole nums
         * */

        _k = k;
        for (int i=0; i<k; i++)
        {
            // note: k could greater than the nums' size
            if(i<nums.size())
            {
                pq.push(nums[i]);
            } else
            {
                break;
            }
        }

        //run through the whole nums
        for (int i=k; i<nums.size(); i++)
        {
            if(pq.top() < nums[i])
            {
                pq.pop();
                pq.push(nums[i]);
            }
        }

    }

    int add(int val) {
        /**
         * 1. if pq 's size is or k, make it k
         * 2. compare the val with the top of the pq, update if needed
         *
         */

        if(pq.empty() || pq.size() < _k)
        {
            pq.push(val);
        } else if (val > pq.top())
        {
            pq.pop();
            pq.push(val);
        }

        return pq.top();
    }
};

int main() {

    int k = 3;
    vector<int> arr{5, -1};
    KthLargest kthLargest(k, arr);

//    ["KthLargest","add","add","add","add","add"]
//    [[3,[5,-1]],[2],[1],[-1],[3],[4]]
    cout << kthLargest.add(2) << endl;   // returns 4
    cout << kthLargest.add(1) << endl;   // returns 5
    cout << kthLargest.add(-1) << endl;  // returns 5
    cout << kthLargest.add(3) << endl;   // returns 8
    cout << kthLargest.add(4) << endl;   // returns 8

    return 0;
}

HashTable & Set

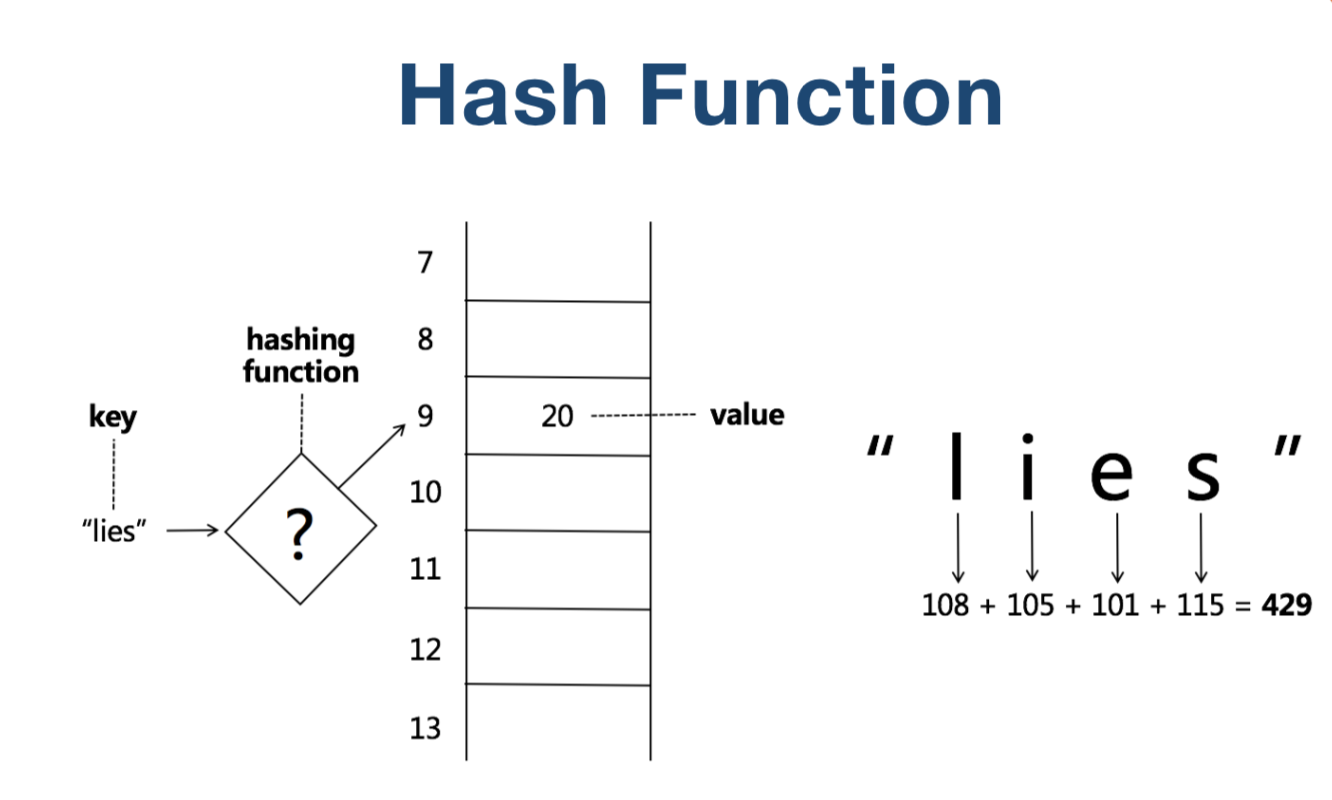
哈希函数

按照一定规律F(e), 计算出数据元素e，特定的哈希值

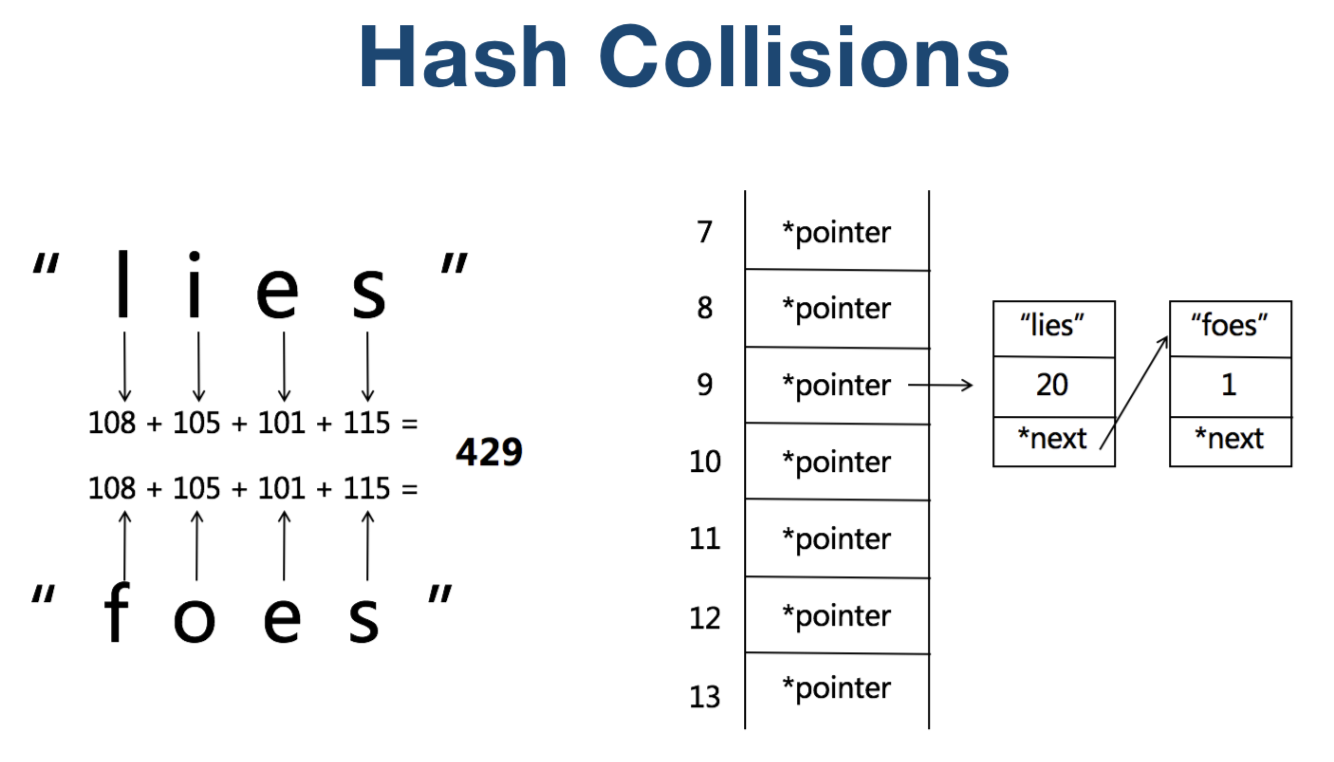
哈希碰撞

不同元素的哈希值可能会一样，这就是哈希碰撞。一般是用拉链法解决，如图，遇到哈希值一样的元素，用链表把后面加入的元素链到上一个哈希值一样的元素后面

编程中用到的dictionary(map) 和 set 中都不会有重复元素。每个元素会有一个特定的哈希值，每次加入新的元素会先确认原先的集合中是否有 哈希值 一样的元素，如果有就不加入新元素，没有就加入。

Binary Search Tree (二叉搜索树)

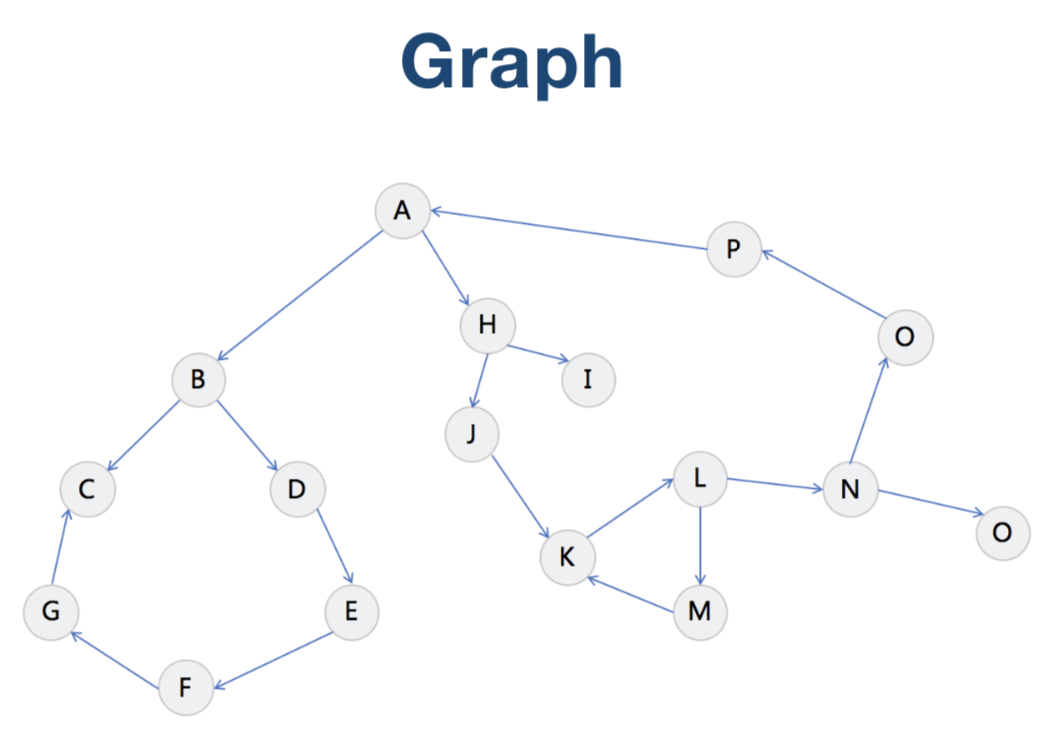
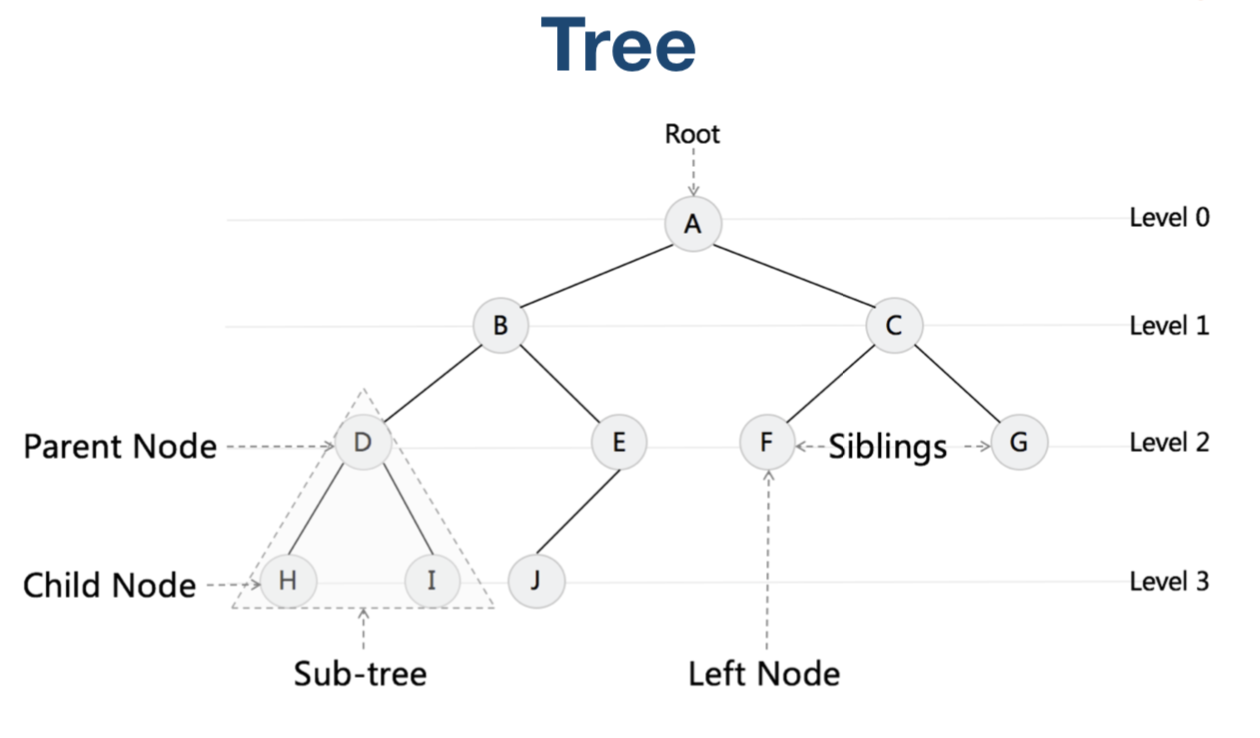
二叉树的结构及各单元的名称， 如下图 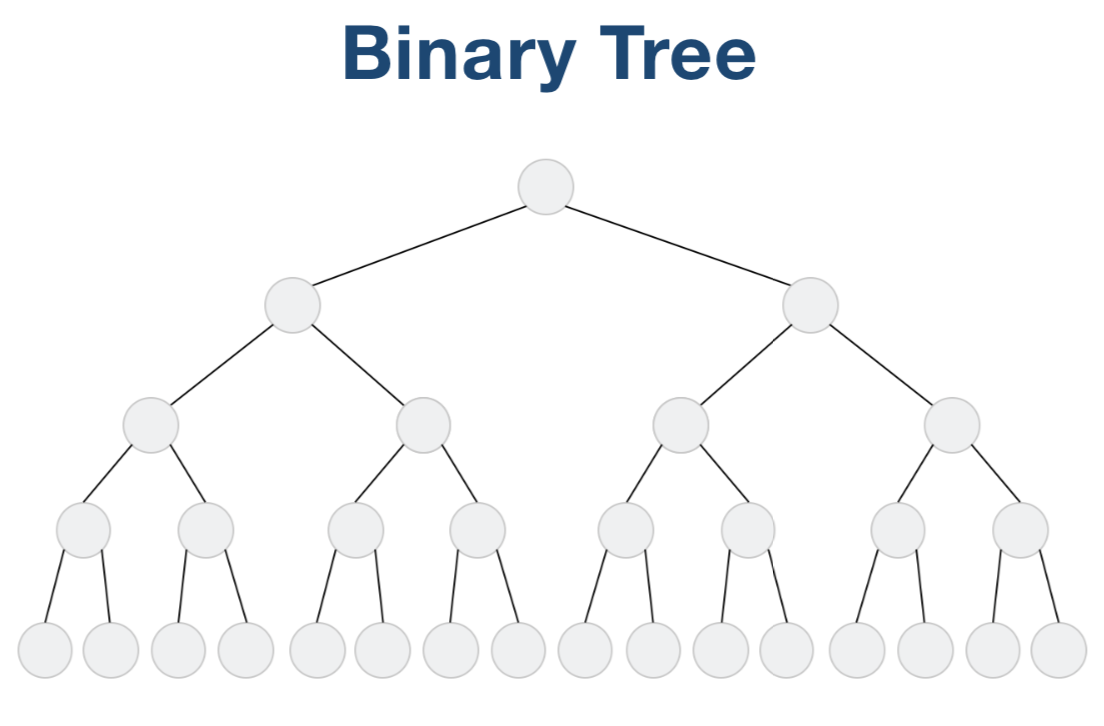链表是特殊的二叉树，二叉树每个节点只有一个子节点时退化成链表 二叉树是特殊的图， 它没有环形结构，每个节点最多只有两个子节点

C++ 实现

struct TreeNode{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
}

二叉搜索树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树（英语：ordered binary tree），排序二叉树（英语 sorted binary tree），是指一棵空树或者具有下列性质的二叉树

  1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值

  2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

  3. 任意节点的左、右子树也分别为二叉查找树。

Traversal Binary Tree (二叉树遍历)

二叉树遍历有三种顺序

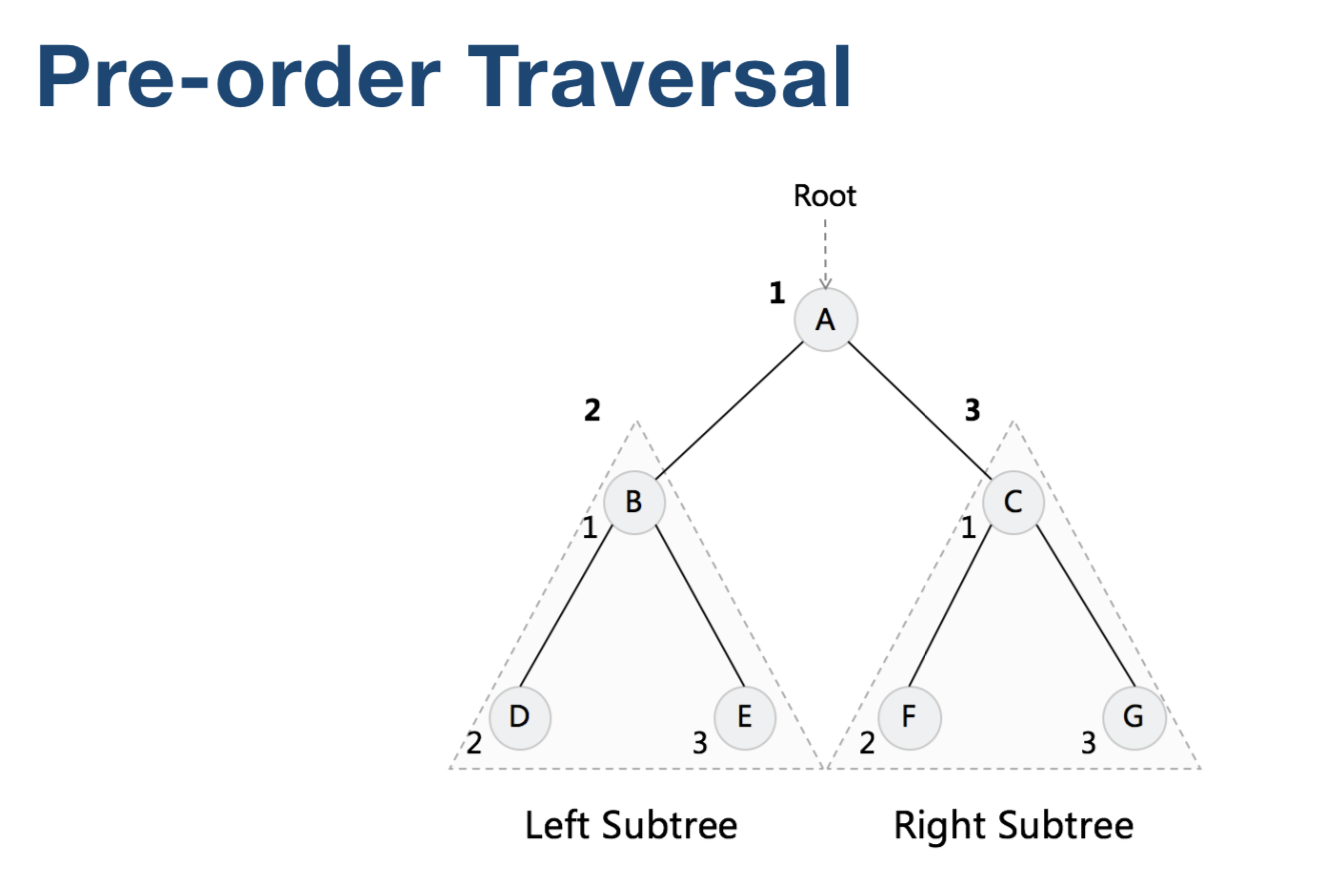
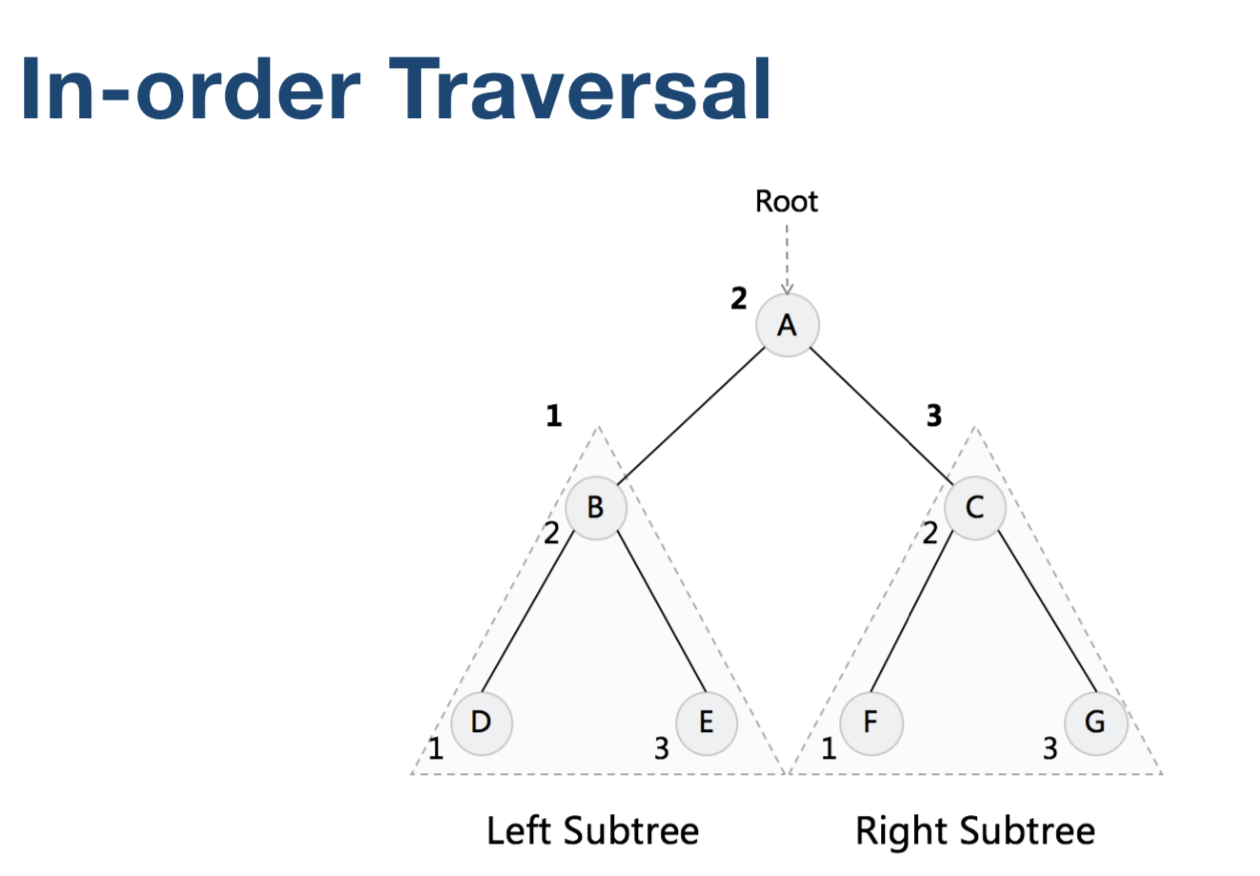
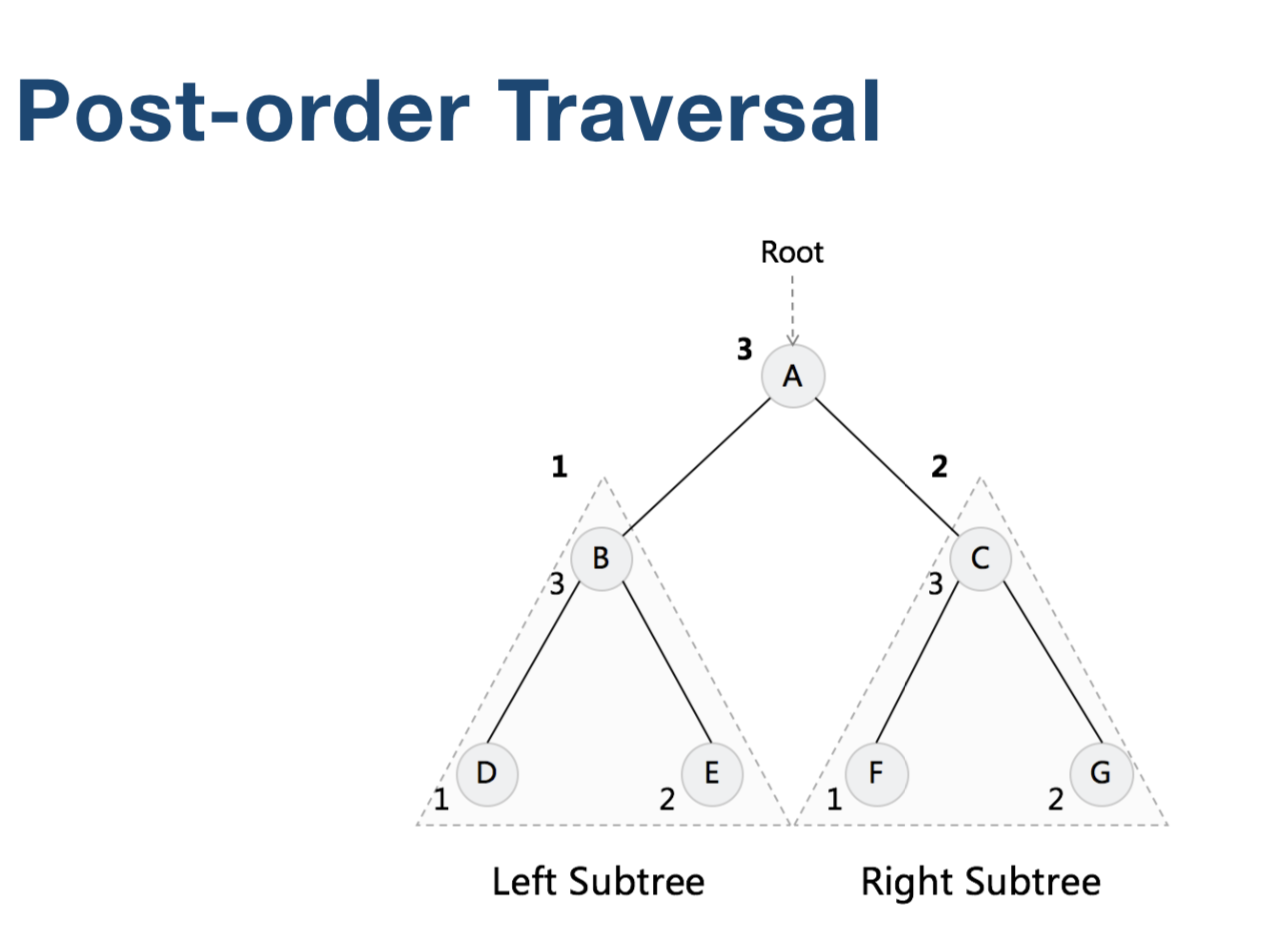
CPP 实现

void preOrder(TreeNode *root, vector<int> &arr)
{
    if (root) {
        arr.push_back(root->val);
        preOrder(root->left, arr);
        preOrder(root->right, arr);
    }
}

void inOrder(TreeNode *root, vector<int> &arr)
{

    if (root) {
        inOrder(root->left, arr);
        arr.push_back(root->val);
        inOrder(root->right, arr);
    }
}

void postOrder(TreeNode *root, vector<int> &arr)
{
    if (root) {
        postOrder(root->left, arr);
        postOrder(root->right, arr);
        arr.push_back(root->val);
    }
}

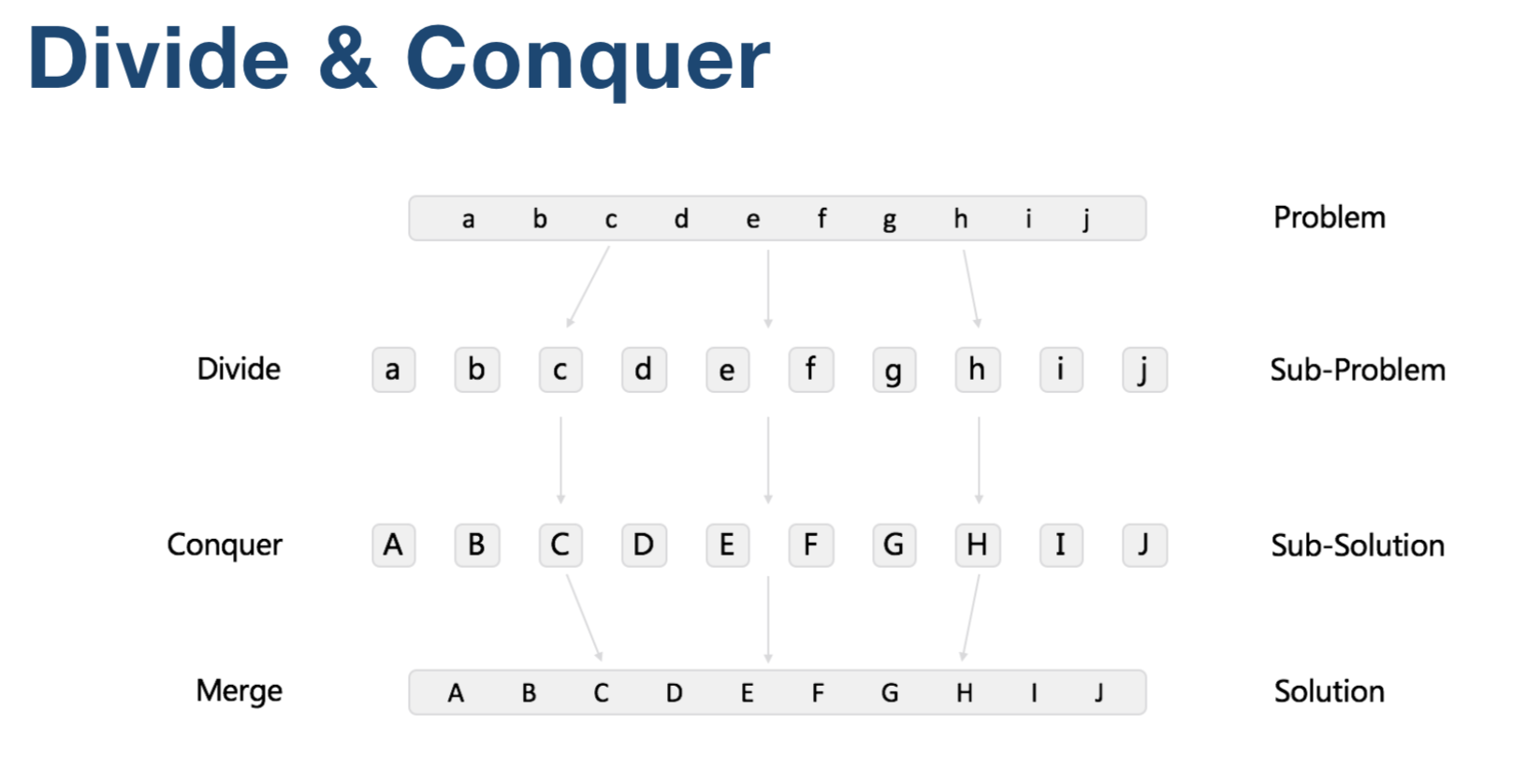
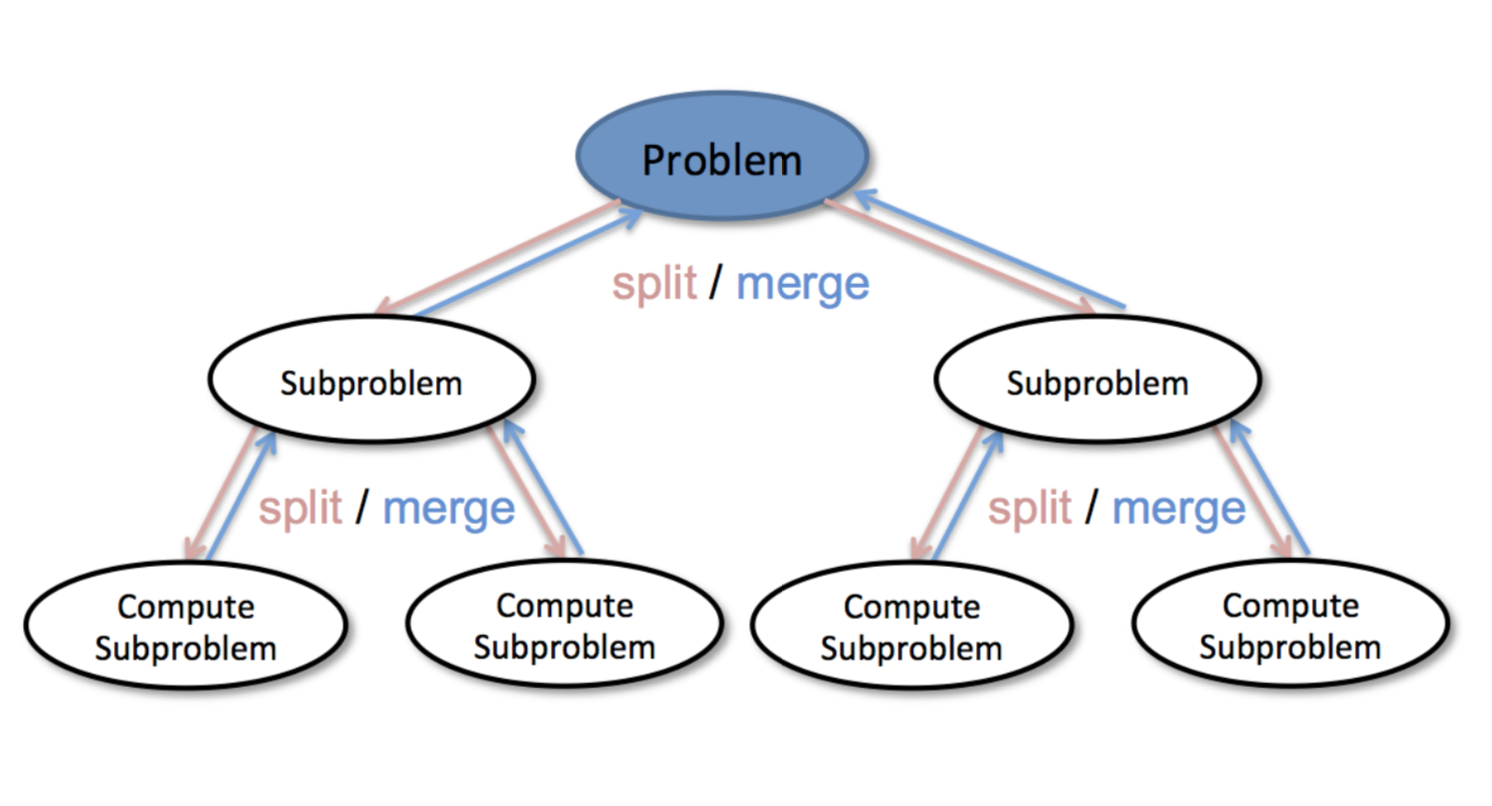
Recursion & (Divide & Conquer) 递归 && 分治

实现伪代码

void recursion(level, param1, param2, ...){
    
    // recursion terminator
    if(level > MAX_LEVEL){
        print_result;
        return
    }

    // process logic in current level
    process_data(level, data, ...);

    // drill down
    self.recursion(level+1, p1, ...);

    // reverse the current level status if needed
    reverse_state(level);

}

递归算法， 必须有一个终止条件， 每次进入函数都去检测是否终止，否则进入递归

result_type divide_conquer(problem, param1, param2, ...){
    
    // recursion terminator
    if (problem == NULL)
    {
        print_result
        return
    }

    // prepare data
    data = prepare_data(problem)
    subProblems = split_problem(problem, data)

    // conquer subproblems
    subresult1 = divide_conquer(subProblems[0], p1, p2, ...)
    subresult2 = divide_conquer(subProblems[1], p1, p2, ...)
    subresult3 = divide_conquer(subProblems[2], p1, p2, ...)
    ...

    // process and generate the final result
    result = process_result(subresult1, subresult2, subresult3, ...)
}

分治： 分而治之，持续分解问题，直到可以解决为止，然后再把结果进行合并