Spark GraphX

Spark GraphX概述

GraphX 是 Spark 一个组件，专门用来表示图以及进行图的并行计算。GraphX 通过重新定义了图的抽象概念来拓展了 RDD: 定向多图，其属性附加到每个顶点和边。
为了支持图计算， GraphX 公开了一系列基本运算符(比如:mapVertices、 mapEdges、subgraph)以及优化后的 Pregel API 变种。此外，还包含越来越多的图算法和构建器，以简化图形分析任务。
GraphX在图顶点信息和边信息存储上做了优化，使得图计算框架性能相对于原生 RDD实现得以较大提升，接近或到达 GraphLab 等专业图计算平台的性能。GraphX 最大的贡献是，在Spark之上提供一栈式数据解决方案，可以方便且高效地完成图计算的一整套流水作业。

图的相关术语

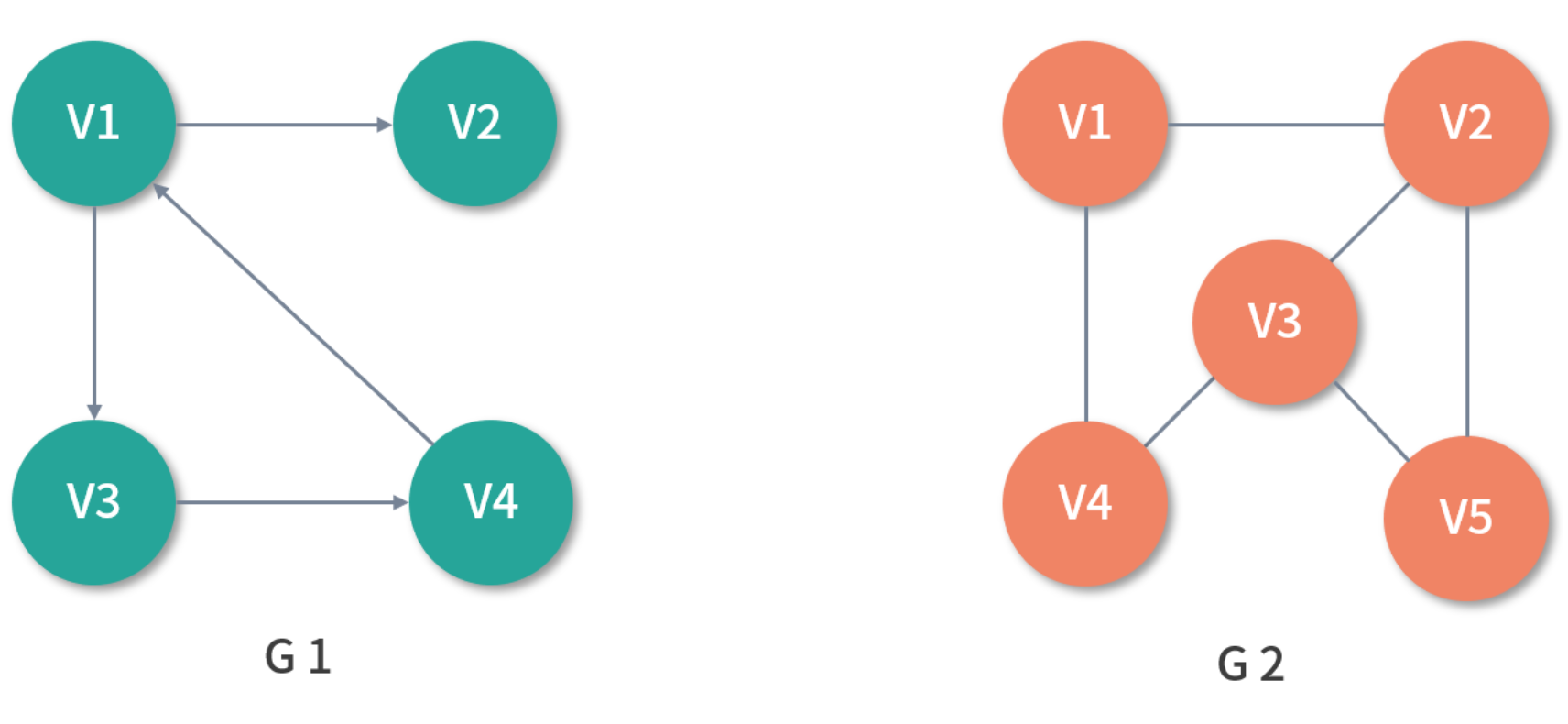
图是一种较线性表和树更为复杂的数据结构，图表达的是多对多的关系。
如上图所示，G1 是一个简单的图，其中 V1、V2、V3、V4 被称作顶点(Vertex)，任意两个顶点之间的通路被称为边(Edge)，它可以由(V1、V2)有序对来表示，这时称 G1 为有向图，意味着边是有方向的，若以无序对来表示图中一条边，则该图为无向图，如 G2。

在 G1 中，与顶点相关联的边的数量被称为顶点的度(Degree)。其中，以顶点为起点的边的数量被称为该顶点的出度(OutDegree)，以顶点为终点的边的数量被称为该顶点的入度(InDegree)。

以 G1 中的 V1 举例，V1 的度为 3，其中出度为 2，入度为 1。在无向图 G2 中，如果任意两个顶点之间是连通的，则称 G2 为连通图(Connected Graph)。在有向图中 G1 中，如果任意两个顶点 Vm、Vn 且 m ≠ n，从 Vm 到 Vn 以及从 Vn 到 Vm 之间都存在通路，则称 G1 为强连通图(Strongly Connected Graph)。任意两个顶点之间若存在通路，则称为路径(Path)，用一个顶点序列表示，若第一个顶点和最后一个顶点相同，则称为回路或者环(Cycle)。

图数据库与图计算

Neo4j 是一个比较老牌的开源图数据库，目前在业界的使用也较为广泛，它提供了一种简单易学的查询语言 Cypher。
Neo4j 是图数据库，偏向于存储和查询。能存储关联关系比较复杂，实体之间的连接丰富。比如社交网络、知识图谱、金融风控等领域的数据。擅长从某个点或某些点出发，根据特定条件在复杂的关联关系中找到目标点或边。如在社交网络中找到某个点三步以内能认识的人，这些人可以认为是潜在朋友。数据量限定在一定范围内，能短时完成的查询就是所谓的OLTP操作。

Neo4j 查询与插入速度较快，没有分布式版本，容量有限，而且一旦图变得非常大，如数十亿顶点，数百亿边，查询速度将变得缓慢。

比较复杂的分析和算法，如基于图的聚类，PageRank 算法等，这类计算任务对于图数据库来说就很难胜任了，主要由一些图挖掘技术来负责。

Pregel 是 Google 于 2010 年在 SIGMOD 会议上发表的《Pregel: A System for Large-Scale Graph Processing》论文中提到的海量并行图挖掘的抽象框架，Pregel 与 Dremel 一样，是 Google 新三驾马车之一，它基于 BSP 模型(Bulk Synchronous Parallel，整体同步并行计算模型)，将计算分为若干个超步(super step)，在超步内，通过消息来传播顶点之间的状态。Pregel 可以看成是同步计算，即等所有顶点完成处理后再进行下一轮的超步，Spark 基于 Pregel 论文实现的海量并行图挖掘框架 GraphX。

图计算模式

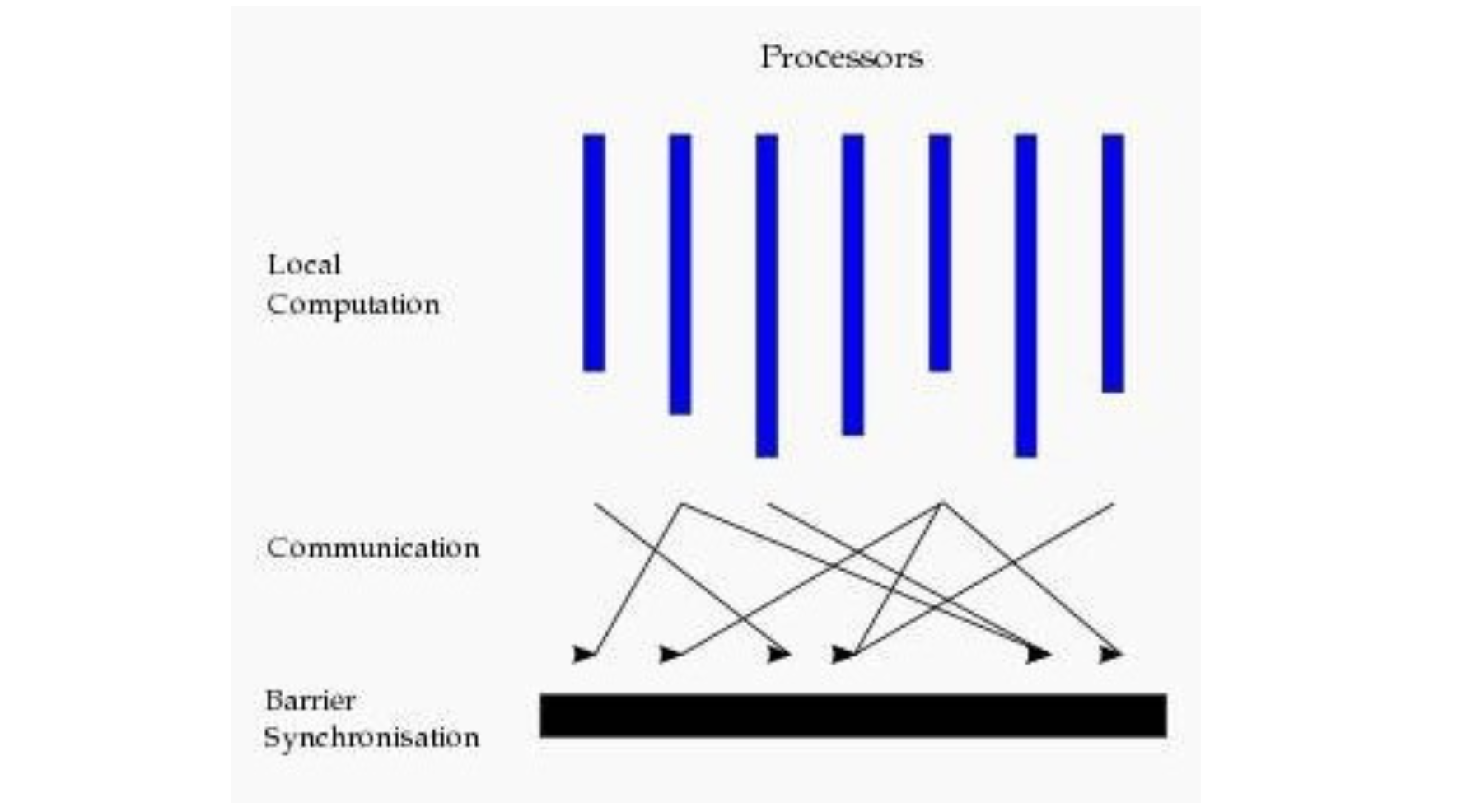
目前基于图的并行计算框架已经有很多，比如来自Google的Pregel、来自Apache开源的图计算框架Giraph / HAMA以及最为著名的GraphLab，其中Pregel、HAMA和 Giraph都是非常类似的，都是基于BSP模式。

BSP即整体同步并行，它将计算分成一系列超步的迭代。从纵向上看，它是一个串行模式，而从横向上看，它是一个并行的模式，每两个超步之间设置一个栅栏 (barrier)，即整体同步点，确定所有并行的计算都完成后再启动下一轮超步。

每一个超步包含三部分内容:

计算compute:每一个processor利用上一个超步传过来的消息和本地的数据进行本地计算
消息传递:每一个processor计算完毕后，将消息传递给与之关联的其它 processors
整体同步点:用于整体同步，确定所有的计算和消息传递都进行完毕后，进入下一个超步

Spark GraphX 基础

GraphX 与 Spark 其他组件相比相对独立，拥有自己的核心数据结构与算子。

GraphX 架构

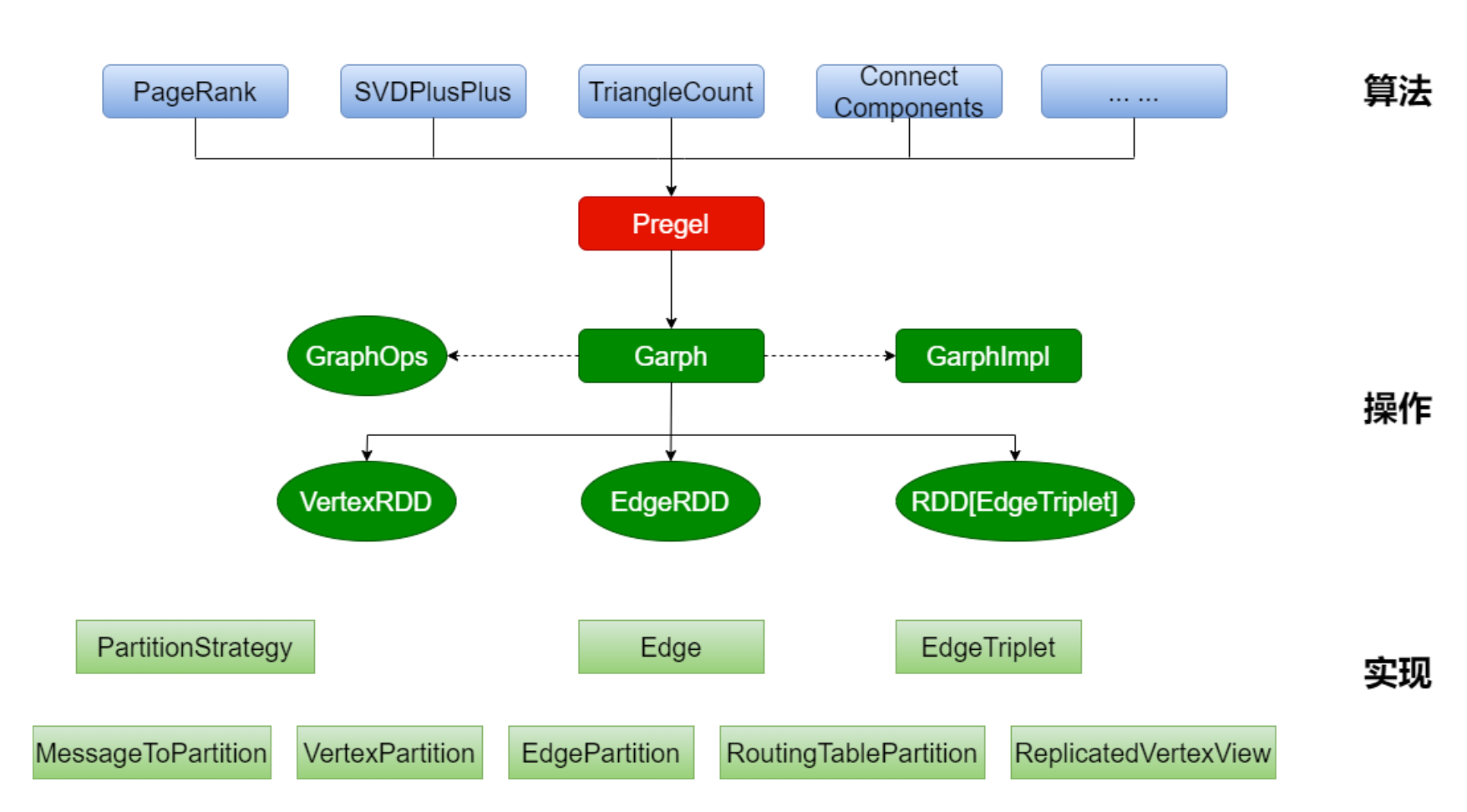
GraphX的整体架构可以分为三个部分:

算法层: 基于 Pregel 接口实现了常用的图算法。包括 PageRank、 SVDPlusPlus、TriangleCount、 ConnectedComponents、 StronglyConnectedConponents 等算法
接口层: 在底层 RDD 的基础之上实现了 Pregel 模型 BSP 模式的计算接口 * 底层: 图计算的核心类，包含:VertexRDD、EdgeRDD、RDD[EdgeTriplet]

存储模式

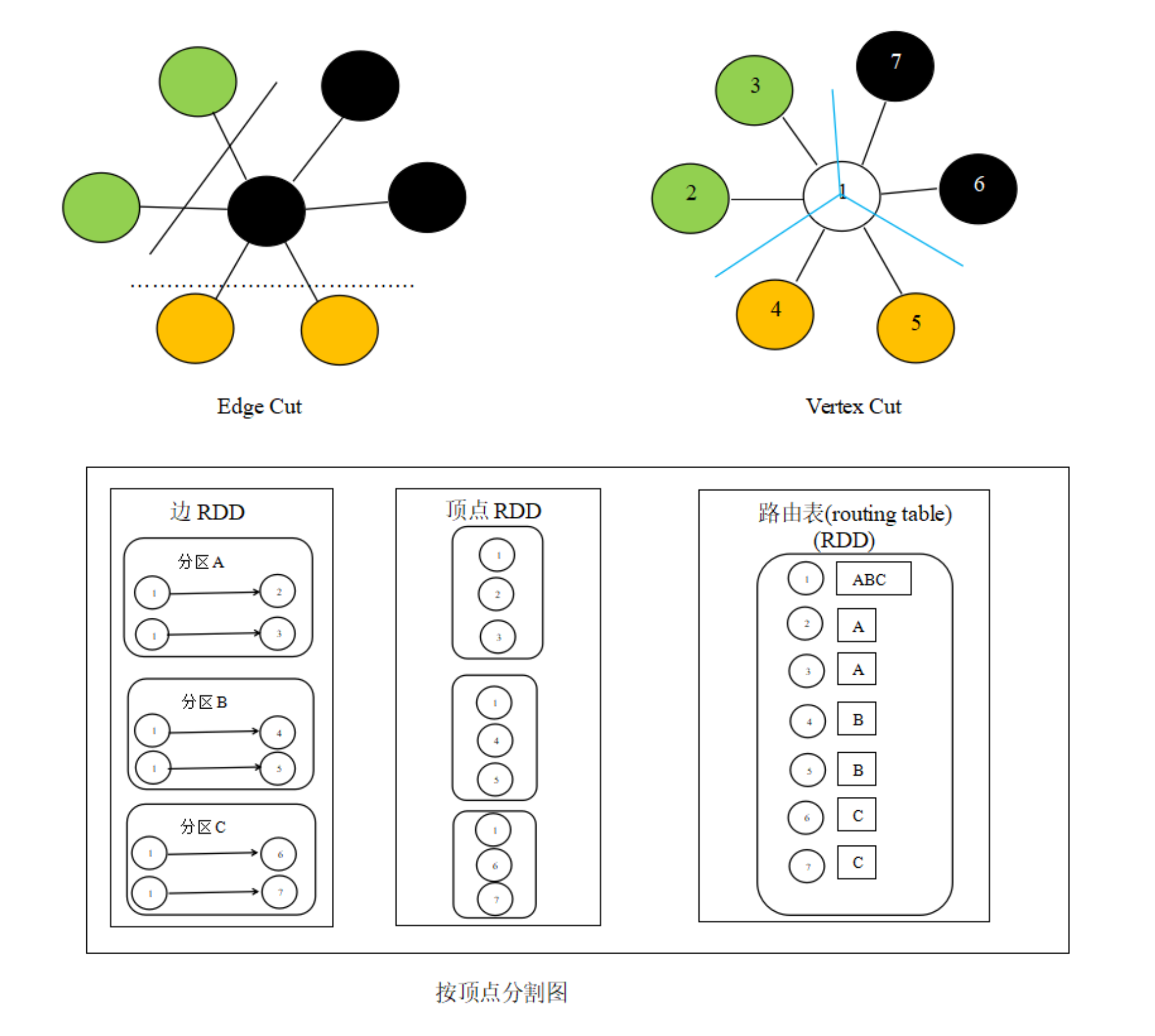
巨型图的存储总体上有边分割和点分割两种存储方式。2013年，GraphLab2.0将其存储方式由边分割变为点分割，在性能上取得重大提升，目前基本上被业界广泛接受并使用。

边分割(Edge-Cut) 每个顶点都存储一次，但有的边会被打断分到两台机器上。这样做的好处是节省存储空间;坏处是对图进行基于边的计算时，对于一条两个顶点被分到不同机器上的边来说，要跨机器通信传输数据，内网通信流量大
点分割(Vertex-Cut) 每条边只存储一次，都只会出现在一台机器上。邻居多的点会被复制到多台机器上，增加了存储开销，同时会引发数据同步问题。好处是可以大幅减少内网通信量
选型虽然两种方法互有利弊，但现在是点分割占上风，各种分布式图计算框架都将自己底层的存储形式变成了点分割。主要原因有以下两个:
- 磁盘价格下降，存储空间不再是问题，而内网的通信资源没有突破性进展，集群计算时内网带宽是宝贵的，时间比磁盘更珍贵。这点就类似于常见的空间换时间的策略;
- 在当前的应用场景中，绝大多数网络都是“无尺度网络”，遵循幂律分布，不同点的邻居数量相差非常悬殊。而边分割会使那些多邻居的点所相连的边大多数被分到不同的机器上，这样的数据分布会使得内网带宽更加捉襟见肘，于是边分割存储方式被渐渐抛弃了;

核心数据结构

GraphX API 的开发语言目前仅支持 Scala。GraphX 的核心数据结构 Graph 由 RDD 封装而成。

Graph
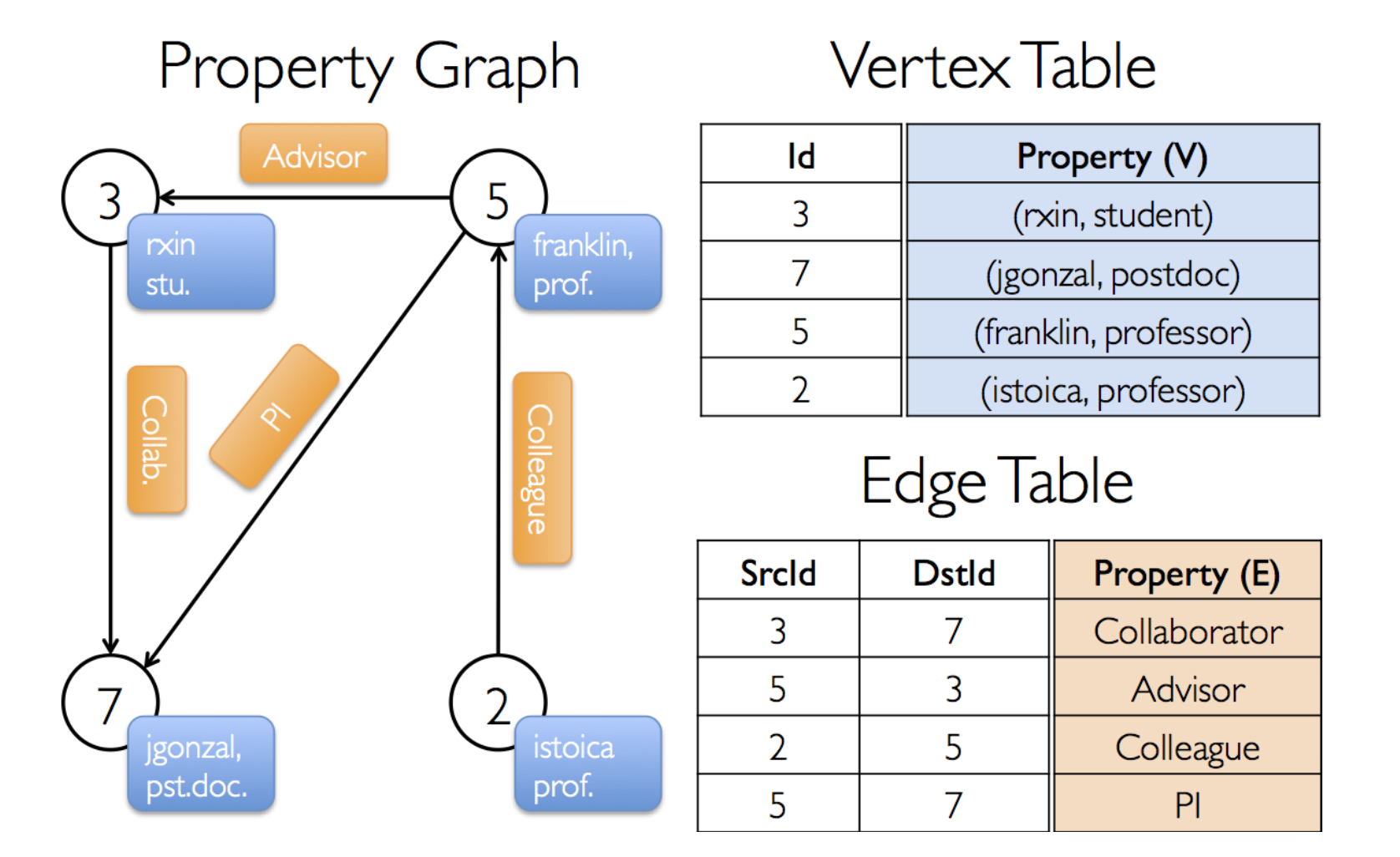GraphX 用属性图的方式表示图，顶点有属性，边有属性。存储结构采用边集数组的形式，即一个顶点表，一个边表，如上图所示。

顶点 ID 是非常重要的字段，它不光是顶点的唯一标识符，也是描述边的唯一手段。顶点表与边表实际上就是 RDD，它们分别为 VertexRDD 与 EdgeRDD
- vertices 为顶点表，VD 为顶点属性类型
- edges 为边表，ED 为边属性类型
- 可以通过 Graph 的 vertices 与 edges 成员直接得到顶点 RDD 与边 RDD
- 顶点 RDD 类型为 VerticeRDD，继承自 RDD[(VertexId, VD)]
- 边 RDD 类型为 EdgeRDD，继承自 RDD[Edge[ED]]
vertices vertices对应着名为 VertexRDD 的RDD。这个RDD由顶点id和顶点属性两个成员变量。
VertexRDD继承自 RDD[(VertexId, VD)]，这里VertexId表示顶点id，VD表示顶点所带的属性的类别。
VertexId 实际上是一个Long类型的数据;
edges edges对应着EdgeRDD。这个RDD拥有三个成员变量，分别是源顶点id、目标顶点id以及边属性。

Edge代表边，由源顶点id、目标顶点id、以及边的属性构成。
triplets
triplets 表示边点三元组，如上图所示(其中圆柱形分别代表顶点属性与边属性)

通过 triplets 成员，用户可以直接获取到起点顶点、起点顶点属性、终点顶点、终点顶点属性、边与边属性信息。triplets 的生成可以由边表与顶点表通过 ScrId 与 DstId 连接而成。

triplets对应着EdgeTriplet。它是一个三元组视图，这个视图逻辑上将顶点和边的属性保存为一个RDD[EdgeTriplet[VD, ED]]。

Spark GraphX计算

引入依赖:

<dependency>  
    <groupId>org.apache.spark</groupId>  
    <artifactId>spark-graphx_2.12</artifactId>  
    <version>${spark.version}</version>  
</dependency>  

图的基本操作

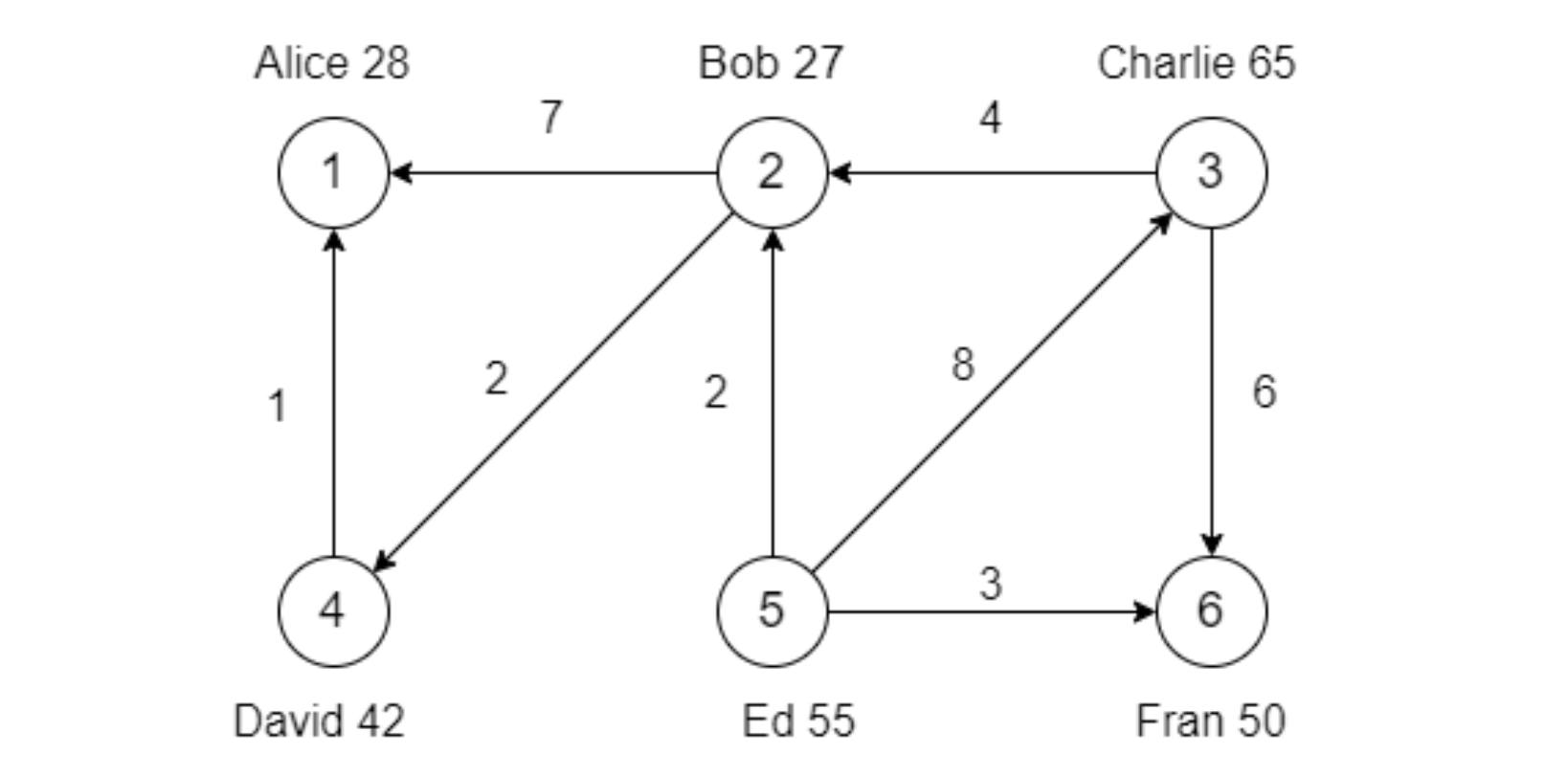
import org.apache.spark.graphx.{Edge, Graph, VertexId}  
import org.apache.spark.rdd.RDD  
import org.apache.spark.{SparkConf, SparkContext}  
    
case class User(name: String, age: Int, inDeg: Int, outDeg: Int)  
    
object GraphXExampleProperties {  
  def main(args: Array[String]): Unit = {  
    val conf = new SparkConf()  
      .setAppName(this.getClass.getCanonicalName.init)  
      .setMaster("local[*]")  
    val sc = new SparkContext(conf)  
    sc.setLogLevel("ERROR")  
    
    // 初始化数据  
    // 定义顶点 (Long, info)  
    val vertexArray: Array[(VertexId, (String, Int))] = Array(  
      (1L, ("Alice", 28)),  
      (2L, ("Bob", 27)),  
      (3L, ("Charlie", 65)),  
      (4L, ("David", 42)),  
      (5L, ("Ed", 55)),  
      (6L, ("Fran", 50))  
    )  
    
    // 定义边 (Long, Long, attr)  
    val edgeArray: Array[Edge[Int]] = Array(  
      Edge(2L, 1L, 7),  
      Edge(2L, 4L, 2),  
      Edge(3L, 2L, 4),  
      Edge(3L, 6L, 6),  
      Edge(4L, 1L, 1),  
      Edge(5L, 2L, 2),  
      Edge(5L, 3L, 8),  
      Edge(5L, 6L, 3)  
    )  
    
    
    // 构造vertexRDD和edgeRDD  
    val vertexRDD: RDD[(VertexId, (String, Int))] = sc.makeRDD(vertexArray)  
    val edgeRDD: RDD[Edge[Int]] = sc.makeRDD(edgeArray)  
    
    // 构造图Graph[VD,ED]  
    val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)  
    
    // 属性操作示例  
    // 找出图中年龄大于30的顶点  
    graph.vertices  
        .filter{case (_, (_, age)) => age>30}  
        .foreach(println)  
    
    // 找出图中属性大于5的边  
    
    graph.edges  
        .filter(_.attr > 5)  
        .foreach(println)  
    
    // 列出边属性>5的triplets  
//    val triplets: RDD[EdgeTriplet[(String, Int), Int]] = graph.triplets  
    graph.triplets  
        .filter(_.attr > 5)  
        .foreach(println)  
    
    // degrees操作  
    // 找出图中最大的出度、入度、度数  
    println("*********** 出度 ***********")  
    val outDegress: (VertexId, Int) = graph.outDegrees.reduce((x, y) => if (x._2 > y._2) x else y)  
    println(s"outDegress = $outDegress")  
    println("*********** 入度 ***********")  
    val inDregree: (VertexId, Int) = graph.inDegrees.reduce((x, y) => if (x._2 > y._2) x else y)  
    println(s"inDregree = $inDregree")  
    println("*********** 度数 ***********")  
    val degree: (VertexId, Int) = graph.degrees.reduce((x, y) => if (x._2 > y._2) x else y)  
    println(s"degree = $degree")  
    
    // 转换操作  
    // 顶点的转换操作。所有人的年龄加 10 岁  
    println("----------------- 顶点的转换操作 -----------------")  
    graph  
      .mapVertices{case (id, (name, age)) => (id, (name, age+100))}  
      .vertices  
      .foreach(println)  
    
    // 边的转换操作。边的属性*2  
    println("----------------- 边的转换操作 -----------------")  
    graph  
      .mapEdges{e => e.attr = e.attr*2; e}  
      .edges  
      .foreach(println)  
    
    // 结构操作  
    // 顶点年龄 > 30 的子图  
    println("*********************** 顶点年龄 > 30 的子图 ***********************")  
//    def vpred(id: VertexId, attr:(String, Int)): Boolean = attr._2 > 30  
    val subGraph = graph.subgraph(vpred = (_, attr) => attr._2 > 30)  
    subGraph.triplets.foreach(println)  
    
        
    // 连接操作  
    println("*********************** 连接操作 ***********************")  
    // 找到 出度=入度 的人员  
    // 直接join的解法  
    graph.vertices  
      .join(  
        graph.inDegrees  
          .join(graph.outDegrees)  
          .filter{case (_, (in, out)) => in == out}  
      )  
      .map{case (id, (attr, _)) => (id, attr)}  
      .foreach(println)  
    
    // 创建一个新图，顶点VD的数据类型为User，并从graph做类型转换  
    var userGraph: Graph[User, Int] = graph  
      .mapVertices { case (_, (name, age)) => User(name, age, 0, 0)}  
    userGraph = userGraph.outerJoinVertices(userGraph.inDegrees) {  
      case (_, user, degree) => User(user.name, user.age, degree.getOrElse(0), user.outDeg)  
    }.outerJoinVertices(userGraph.outDegrees) {  
      case (_, user, degree) => User(user.name, user.age, user.inDeg, degree.getOrElse(0))  
    }  
    userGraph.vertices  
      .filter{case (_, user) => user.inDeg==user.outDeg}  
      .foreach(println)  
    
    // 聚合操作  
    // 找出5到各顶点的最短距离  
    println("*********************** 聚合操作 ***********************")  
    val sourceId: VertexId = 5L  
    val initialGraph: Graph[Double, Int] = graph.mapVertices((id, _) => if (id==sourceId) 0.0 else Double.PositiveInfinity)  
    
    /**  
     * def pregel[A: ClassTag](  
     * initialMsg: A,  
     * maxIterations: Int = Int.MaxValue,  
     * activeDirection: EdgeDirection = EdgeDirection.Either)(  
     * vprog: (VertexId, VD, A) => VD,  
     * sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],  
     * mergeMsg: (A, A) => A)  
     * : Graph[VD, ED]  
     */  
      // 每次迭代都在遍历edges  
    val distGraph: Graph[Double, Int] = initialGraph.pregel[Double](Double.PositiveInfinity)(  
      // 两个消息来的时候，取它们当中路径的最小值  
      vprog = (_, dist, newDist) => math.min(dist, newDist),  
    
      // Send Message函数  
      // 比较 triplet.srcAttr + triplet.attr和 triplet.dstAttr。  
      // 如果 小于，则发送消息到目的顶点  
      sendMsg = triplet => {  
        if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {  
          Iterator((triplet.dstId, triplet.srcAttr+triplet.attr))  
        } else {  
          Iterator.empty  
        }  
      },  
      mergeMsg = (a, b) => math.min(a, b)  
    )  
    
    printPregelProcess(initialGraph)  
    println()  
    distGraph.vertices.sortBy(_._1).collect().foreach(println)  
    
    sc.stop()  
  }  
    
  /**  
   * 每迭代一步，打印一次  
   * @param initGraph  
   */  
  def printPregelProcess(initGraph:Graph[Double, Int]):Unit = {  
    
    var preGraph = initGraph  
    for (i <- 0.to(2)) {  
      preGraph = preGraph.pregel[Double](Double.PositiveInfinity, maxIterations = 1)(  
    
        vprog = (_, dist, newDist) => math.min(dist, newDist),  
        sendMsg = triplet => {  
          if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {  
            Iterator((triplet.dstId, triplet.srcAttr+triplet.attr))  
          } else {  
            Iterator.empty  
          }  
        },  
        mergeMsg = (a, b) => math.min(a, b)  
      )  
    
      println(s"------------- $i --------------")  
      preGraph.vertices.sortBy(_._1).collect().foreach(println)  
    }  
    
    /**  
     * ------------- 0 --------------  
     * (1,Infinity)  
     * (2,2.0)  
     * (3,8.0)  
     * (4,Infinity)  
     * (5,0.0)  
     * (6,3.0)  
     * ------------- 1 --------------  
     * (1,9.0)  
     * (2,2.0)  
     * (3,8.0)  
     * (4,4.0)  
     * (5,0.0)  
     * (6,3.0)  
     * ------------- 2 --------------  
     * (1,5.0)  
     * (2,2.0)  
     * (3,8.0)  
     * (4,4.0)  
     * (5,0.0)  
     * (6,3.0)  
     */  
  }  
}  
    

pregel的理解
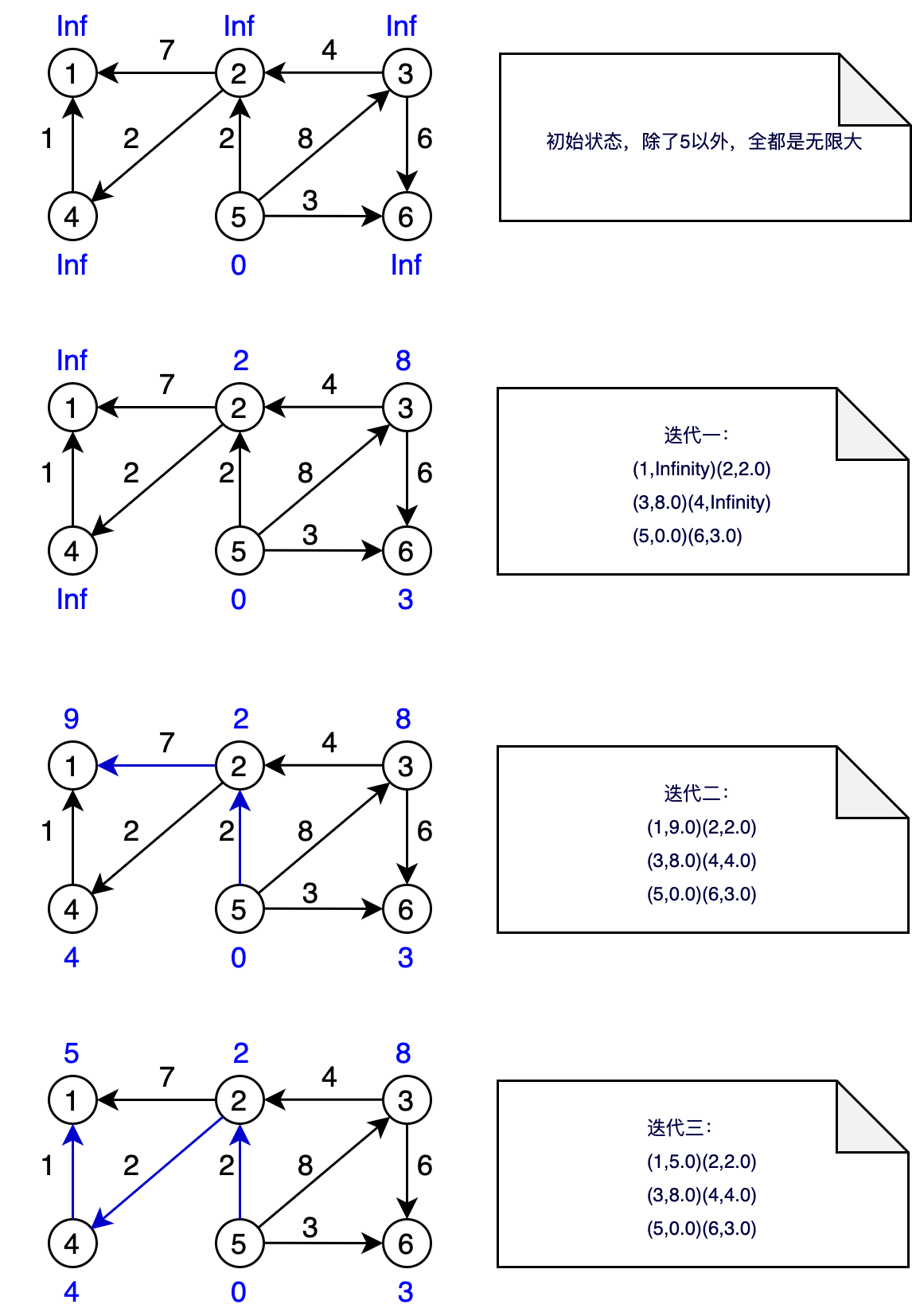上图对应了pregel的每一个超步，每次迭代都扫描所有edges，然后更新vertice，思路和动态规划有点像

Pregel API
图本身是递归数据结构，顶点的属性依赖于它们邻居的属性，这些邻居的属性又依赖于自己邻居的属性。
所以许多重要的图算法都是迭代的重新计算每个顶点的属性，直到满足某个确定的条件。
一系列的图并发抽象被提出来用来表达这些迭代算法。

连通图算法
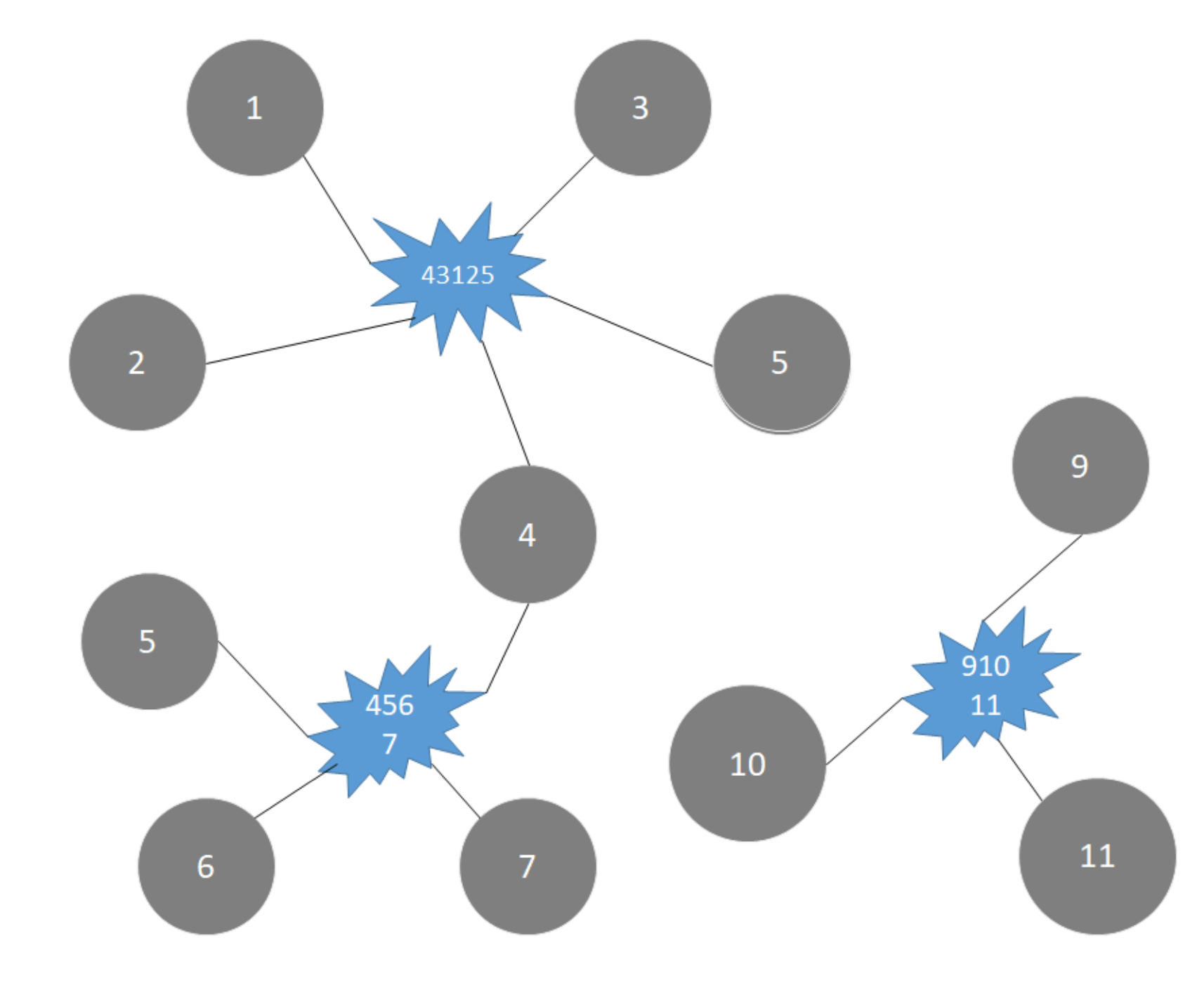给定数据文件，找到存在的连通体

import org.apache.spark.graphx.{Graph, GraphLoader}  
import org.apache.spark.{SparkConf, SparkContext}  
    
object GraphXExample2 {  
  def main(args: Array[String]): Unit = {  
    val conf = new SparkConf()  
      .setAppName(this.getClass.getCanonicalName.init)  
      .setMaster("local[*]")  
    val sc = new SparkContext(conf)  
    sc.setLogLevel("ERROR")  
    
   // 从数据文件中加载，生成图  
    val graph: Graph[Int, Int] = GraphLoader.edgeListFile(sc, "data/graph.dat")  
    graph.vertices.foreach(println)  
    graph.edges.foreach(println)  
    
    println("*"*40)  
  	  
  // 计算连通图  
    graph.connectedComponents()  
        .vertices  
        .sortBy(_._2)  
        .collect()  
        .foreach(println)  
    
    /**  
     * value 是同一个连通图里边最小的id  
     * (4,1)  
     * (431250,1)  
     * (6,1)  
     * (2,1)  
     * (45067,1)  
     * (1,1)  
     * (3,1)  
     * (7,1)  
     * (5,1)  
     *  
     * (10,9)  
     * (11,9)  
     * (9,9)  
     * (9111,9)  
     */  
    
    sc.stop()  
  }  
}  
    

寻找相同的用户，合并信息
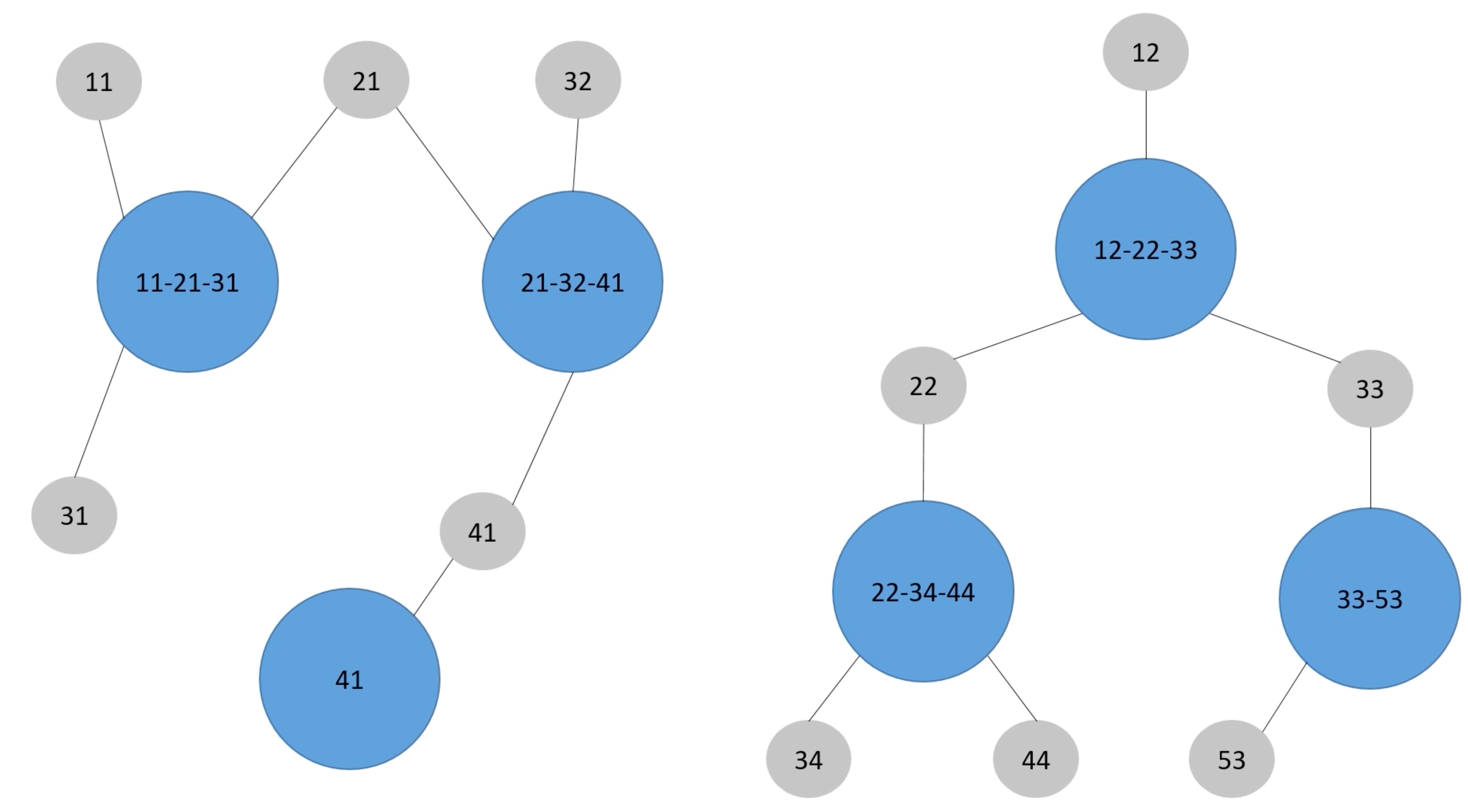借助连通图算法，把数据进行变换之后可以得到上图那样的关联

import org.apache.spark.graphx.{Edge, Graph, VertexId}  
import org.apache.spark.rdd.RDD  
import org.apache.spark.{SparkConf, SparkContext}  
    
/**  
 * 假设:  
 * 假设有五个不同信息可以作为用户标识，分别为:1X、2X、3X、4X、5X;  
 * 每次可以选择使用若干为字段作为标识  
 * 部分标识可能发生变化，如:12 => 13 或 24 => 25  
 *  
 * 根据以上规则，判断以下标识是否代表同一用户:  
 * 11-21-32、12-22-33 (X)  
 * 11-21-32、11-21-52 (OK)  
 * 21-32、11-21-33 (OK)  
 * 11-21-32、32-48 (OK)  
 *  
 * 问题:  
 * 在以下数据中，找到同一用户，合并相同用户的数据  
 * 对于用户标识(id):合并后去重  
 * 对于用户的信息:key相同，合并权重  
 */  
object GraphXExample3 {  
  def main(args: Array[String]): Unit = {  
    val conf = new SparkConf()  
      .setAppName(this.getClass.getCanonicalName.init)  
      .setMaster("local[*]")  
    val sc = new SparkContext(conf)  
    sc.setLogLevel("ERROR")  
    
    // 定义数据  
    val dataRDD: RDD[(List[Long], List[(String, Double)])] =  
      sc.makeRDD(List(  
        (List(11L, 21L, 31L), List("kw$北京" -> 1.0, "kw$上海" -> 1.0, "area$中关村" -> 1.0)),  
        (List(21L, 32L, 41L), List("kw$上海" -> 1.0, "kw$天津" -> 1.0, "area$回龙观" -> 1.0)),  
        (List(41L), List("kw$天津" -> 1.0, "area$中关村" -> 1.0)),  
        (List(12L, 22L, 33L), List("kw$大数据" -> 1.0, "kw$spark" -> 1.0, "area$西二旗" -> 1.0)),  
        (List(22L, 34L, 44L), List("kw$spark" -> 1.0, "area$五道口" -> 1.0)),  
        (List(33L, 53L), List("kw$hive" -> 1.0, "kw$spark" -> 1.0, "area$西二旗" -> 1.0))  
      ))  
    
    // 生成edges  
    val edgesRDD: RDD[Edge[Int]] = dataRDD.flatMap{case (ids, _) =>  
      ids.map(id => id -> ids.mkString.toLong)  
    }.map{case (a, b) => Edge(a, b, 0)}  
    
    // 使用强联通体，进行分组  
    val connectedGraph: Graph[VertexId, Int] =  
      Graph.fromEdges(edgesRDD, 0).connectedComponents()  
    
    connectedGraph.vertices.sortBy(_._2).collect.foreach(println)  
    
    println("-"*50)  
    
    // 定点数据  
    val vertexRDD: RDD[(VertexId, (List[VertexId], List[(String, Double)]))] =  
      dataRDD.map { case (ids, infos) => (ids.mkString.toLong, (ids,infos)) }  
    
    // 关联，并使用联通体的value作为分组依据，后面再进行数据合并处理  
    val resultRDD: RDD[(List[VertexId], List[(String, Double)])] =  
      connectedGraph.vertices  
      .join(vertexRDD)  
      .map{case (_, values) => values}  
      .reduceByKey{  
        case ((bufIds, bufInfos),(ids, infos)) => {  
          // 数据合并处理  
          val newIds: List[VertexId] = (bufIds:::ids).distinct  
          val newInfos: List[(String, Double)] = (bufInfos:::infos)  
            .groupBy(_._1)  
            .map{case (key, values) => (key, values.map(_._2).sum)}  
            .toList  
    
          (newIds, newInfos)  
        }  
      }.map(_._2)  
    
    resultRDD.foreach(println)  
    
    /**  
     * (List(41, 21, 32, 11, 31),List((area$中关村,2.0), (kw$北京,1.0), (kw$天津,2.0), (kw$上海,2.0), (area$回龙观,1.0)))  
     * (List(33, 53, 12, 22, 34, 44),List((kw$大数据,1.0), (kw$spark,3.0), (area$五道口,1.0), (area$西二旗,2.0), (kw$hive,1.0)))  
     */  
    
    sc.stop()  
  }  
}  
    