算法:递归,贪心,分治,动态规划
递归
递归:函数(方法)直接或间接调用自身。是一种常用的编程技巧。
严格来说递归不算一种编程思想,其实最多算是一种编程技巧!
斐波那契数列
斐波那契数列:1、1、2、3、5、8、13、21、34、……
f(1) = 1, f(2) = 1, f(n)=f(n-1)+f(n-2) ( n>=3 )
递归的实现
def fib1(n: Int):Int = {
if (n <= 1) n else fib1(n-1)+fib1(n-2)
// if (n <= 2) n 定义了递归基,如果小于2的情况终止递归
// fib1(n-1)+fib1(n-2) 递归调用
}
上面的实现非常简洁,但是效率较低,根据递推式 T n = T (n − 1) + T(n − 2) + O(1),可得知
- 时间复杂度:O(2^n)
- 空间复杂度: O(n)
- 递归调用的空间复杂度 = 递归深度 * 每次调用所需的辅助空间
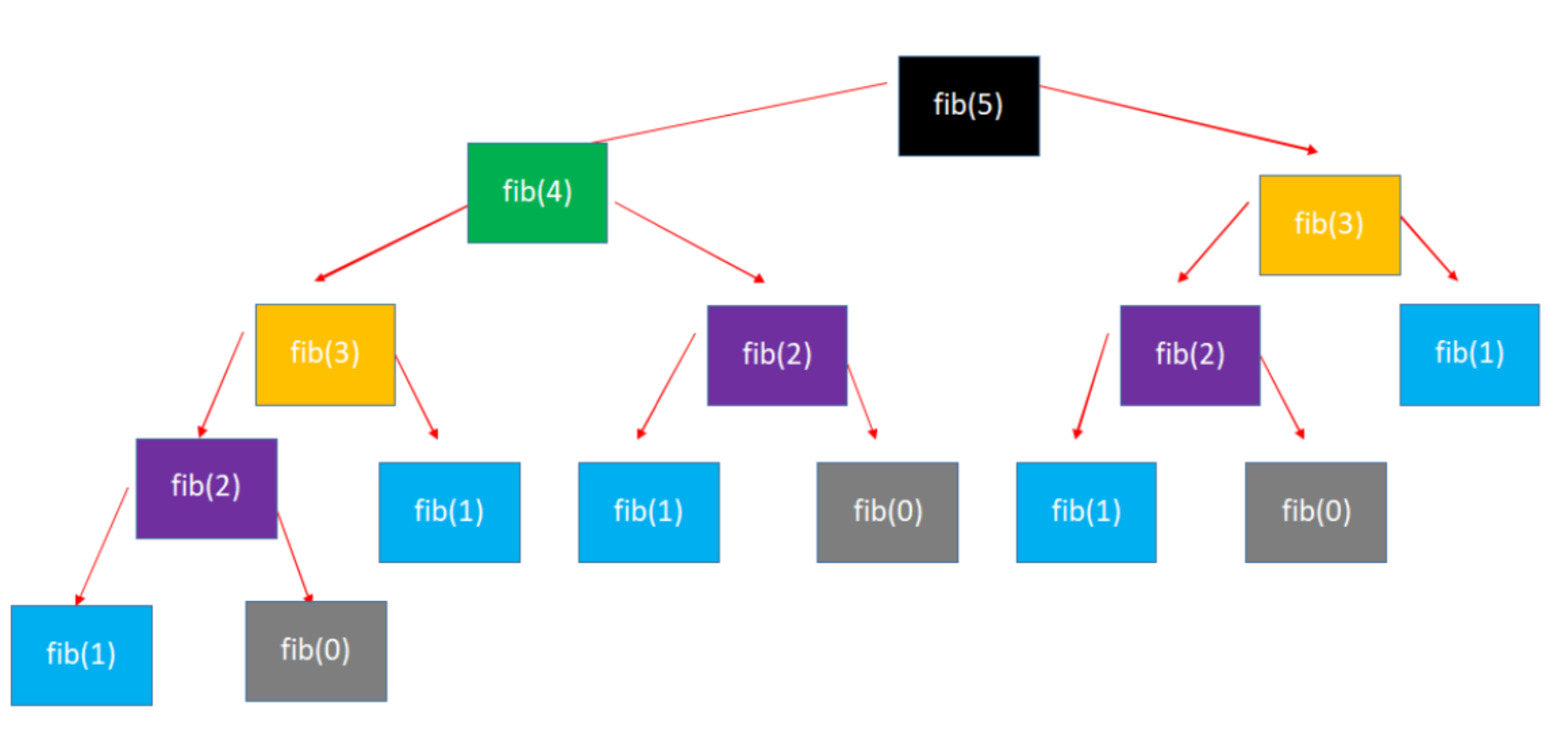
时间复杂度高的原因是出现了大量重复调用,计算fib(5)的时候左边(fib(4))的分支会从fib(0)开始推算到fib(3), 右边的分支(fib(3))又会从fib(0)开始推算到fib(3)…
优化方案:避免重复计算,之前计算过的值不在计算,可以使用数组缓存起来
// 使用数组
def fib2(n: Int):Int = {
// 不需要递推的情况
if (n <= 1) return n
val list = new Array[Int](n+1)
// 递推基
list(1) = 1
for (i <- 2 to n) {
list(i) = list(i-1) + list(i-2)
}
list.last
}
上面的代码还可以进一步优化,因为其实每次只需要用到数组的最后两个元素,那只定义两个变量用来缓存数据就可以了
// 使用变量
def fib3(n: Int):Int = {
if (n <= 1) return n
var first = 0
var second = 1
for (_ <- 2 to n) {
second = first+second
first = second-first
}
second
}
思考🤔
递归效率不高,为何还使用递归?
使用递归往往不是为了求得最优解,是为了简化解决问题的思路,代码会更简洁!!
先得出正确答案,然后再从递归的解法推导出递推的解法
评价算法
对于同一个问题可以多种解决方式,也就是同一个问题可以有多种算法可以解决,那我们不禁要问:
不同的算法它们的效率一样吗?
答案是肯定不一样,使用不同的算法解决同一个问题,效率可能相差非常大!😱
事后统计法
比较不同算法对同一组输入数据的处理时间,被称为事后统计法
需要编写效率统计工具,用来评估算法的效率
// java
import java.text.SimpleDateFormat;
import java.util.Date;
public class Times {
private static final SimpleDateFormat fmt = new SimpleDateFormat("HH:mm:ss.SSS");
public interface Task {
void execute();
}
public static void test(String name, Task task) {
if (task == null) return;
name = (name == null) ? "" : ("[ " + name + " ]");
System.out.println(name);
System.out.println("begin : " + fmt.format(new Date()));
long begin = System.currentTimeMillis();
task.execute();
long end = System.currentTimeMillis();
System.out.println("end: " + fmt.format(new Date()));
double delta = (end - begin)/1000.0;
System.out.println("duration: " + delta + " s");
System.out.println("---------------------------------------------");
}
}
事后统计法缺点
-
执行时间取决于硬件以及运行时各种不确定的环境因素(开启很多软件与没开启很多软件)
-
必须编写测试代码
-
测试数据的选择比较难保证公正性(有些算法数据量小可能快,大了就不行,有些相反)
通常从以下维度来评估算法的优劣
- 正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)
- 时间复杂度(Time complexity):估算程序指令的执行次数(执行时间)
- 空间复杂度(Space complexity):估算所需占用的存储空间
大O表示法(Big O)
大O表示法的定义:一般用大O表示法来描述算法复杂度,它表示的是算法对于数据规模 n的复杂度(时间复杂度,空间复杂度)
常见复杂度
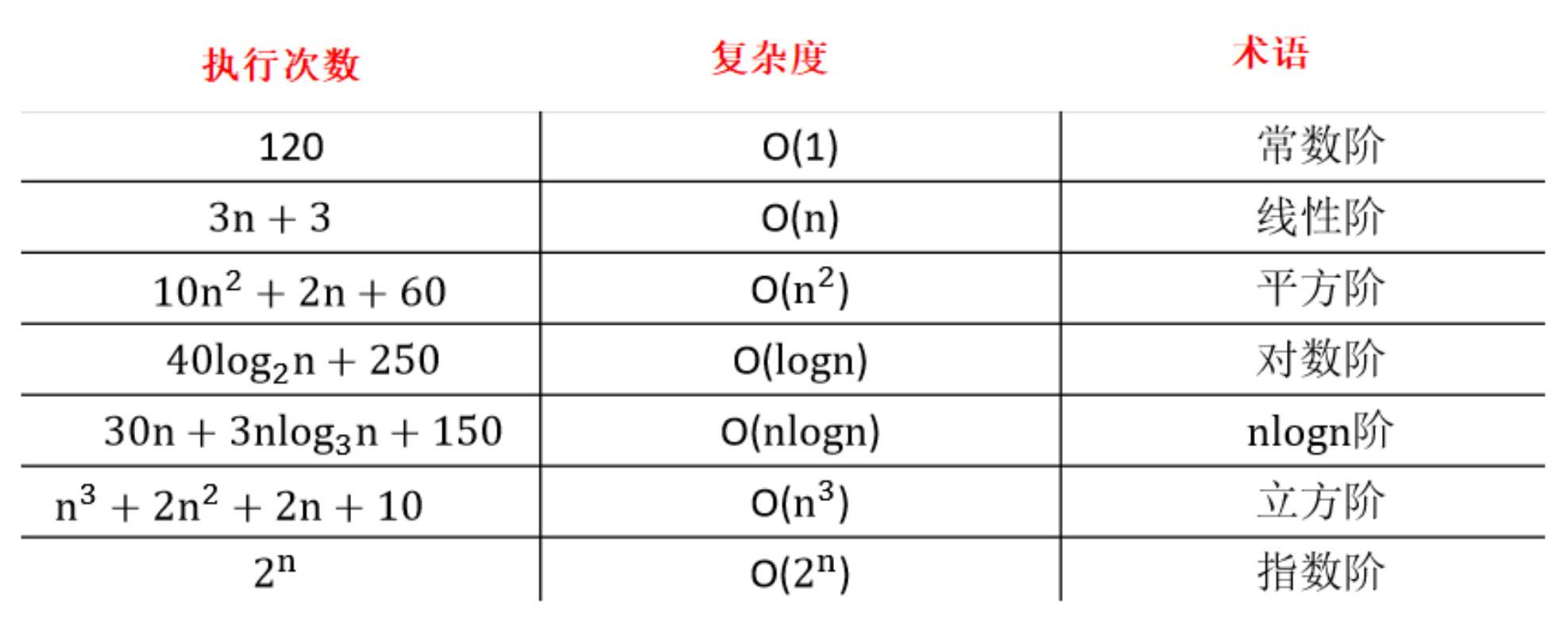
时间复杂度的优先级
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
优化算法主要是优化时间复杂度的级别
复杂度曲线图
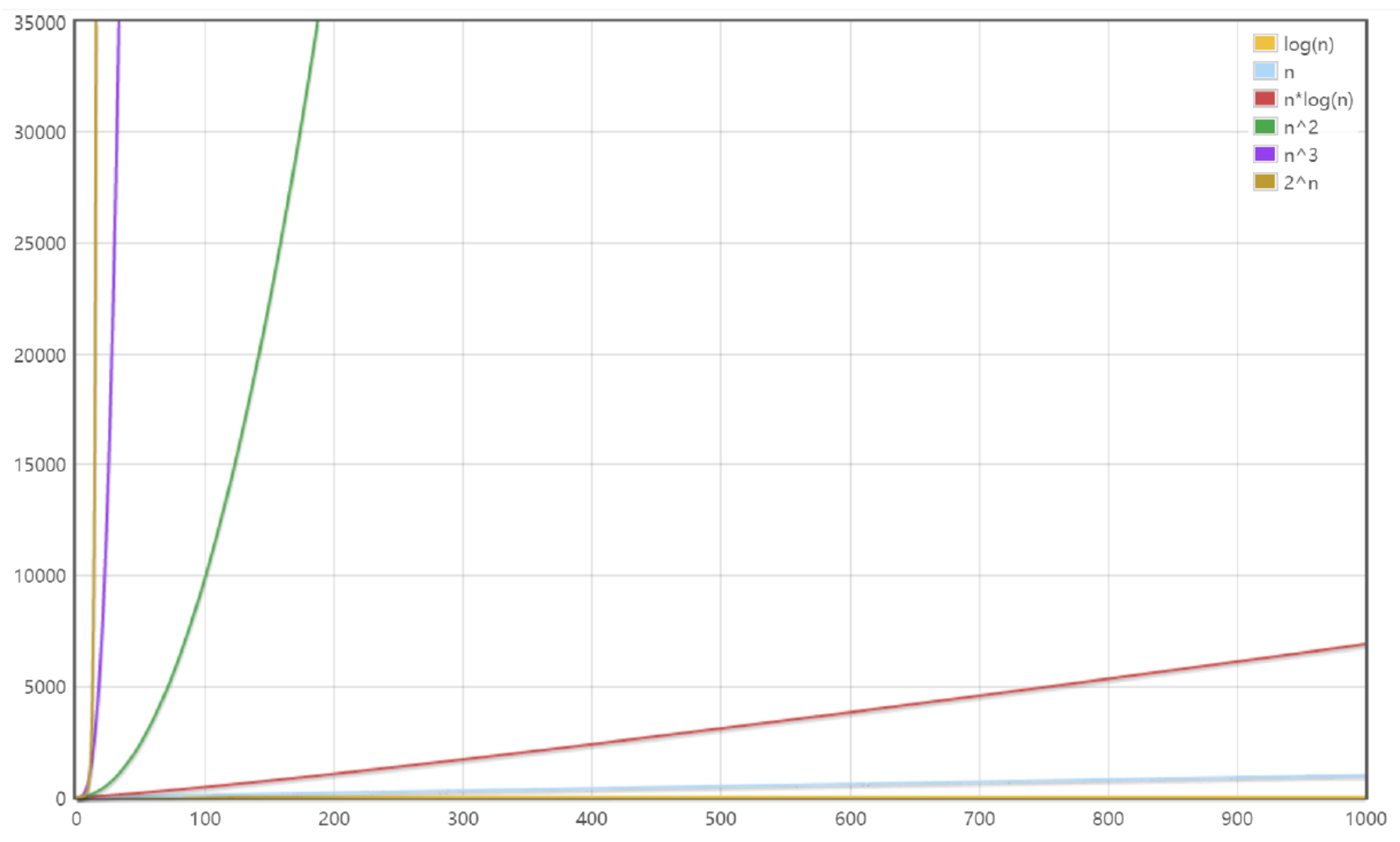
空间复杂度
空间复杂度是估算大概占用的存储空间
对于当前的算法程序来说我们更关注的时间复杂度,因为现在硬件资源都很充足!
补充:注意大O表示法是估算,所谓的执行次数并不是我们的代码执行次数,因为代码最终都要转为汇编的指令,可能就不仅仅是我们代码的执行次数了。但是这种差异大概都一样而且是常数级别,所以不影响大O表示法的最终结果,大O表示法主要看量级
估算斐波那契实现复杂度
def fib1(n: Int):Int = {
if (n <= 1) n else fib1(n-1)+fib1(n-2)
}
// 时间复杂度:O(2^n)
// 空间复杂度:O(n)
def fib2(n: Int):Int = {
// 不需要递推的情况
if (n <= 1) return n
val list = new Array[Int](n+1)
// 递推基
list(1) = 1
for (i <- 2 to n) {
list(i) = list(i-1) + list(i-2)
}
list.last
}
// 时间复杂度:O(n)
// 空间复杂度:O(n)
def fib3(n: Int):Int = {
if (n <= 1) return n
var first = 0
var second = 1
for (_ <- 2 to n) {
second = first+second
first = second-first
}
second
}
// 时间复杂度:O(n)
// 空间复杂度:O(1)
算法优化角度
- 尽可能少的执行时间
- 尽可能少的存储空间
- 根据情况,可以空间换时间 时间换空间
递归基本思想
递归的基本思想就是拆解问题,通过下图理解递归的思想
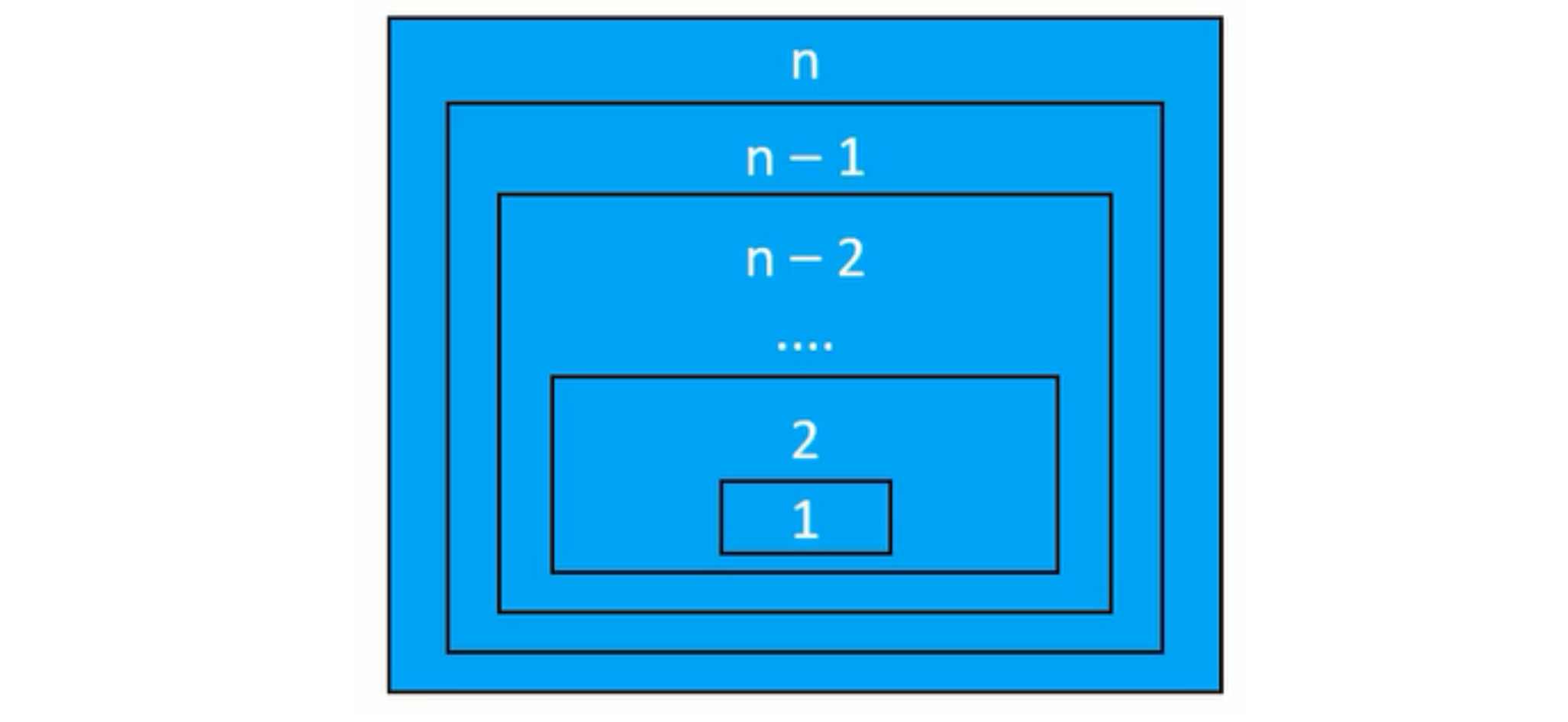
- 拆分问题
- 把规模大的问题编程规模较小的同类型问题
- 规模较小的问题又不断变成规模更小的问题
- 规模小到一定程度就可以直接得到结果
- 求解
- 由最小规模问题的解推导出较大规模问题的解
- 由较大规模问题的解不断推导出规模更大问题的解
- 最后推导出原来问题的解
总结:从人生目标递推到今天要做什么,然后一步步迈向人生巅峰
递归使用步骤与技巧
-
确定函数的功能:第一步先不要思考函数里面代码逻辑如何实现,先搞清楚这个函数的目的,完成什么事情?
-
确定子问题与原问题的关系:找到 f(n) 与 f(n – 1) 的关系
-
明确递归基(边界条件)
-
递归的过程中,问题的规模在不断减小,当问题缩减到一定程度便可以直接得出它的解
-
寻找递归基,等价于:问题规模小到什么程度可以直接得出解?
-
跳台阶
题目:楼梯有 n 阶台阶,上楼可以一步上 1 阶,也可以一步上 2 阶,走完 n 阶台阶共有多少种不同的走法?
object StairDemo {
def main(args: Array[String]): Unit = {
for (i <- 1 to 5) {
println(s"$i - ${stair(i)}")
}
}
/**
* 楼梯有 n 阶台阶,上楼可以一步上 1 阶,
* 可以一步上 2 阶,走完 n 阶台阶共有多少种不同的走法?
* @param n
* @return
*/
def stair(n: Int):Int = {
/**
* 假设第一次走 1 阶,还剩 n – 1 阶,共 f(n – 1) 种走法
* 假设第一次走 2 阶,还剩 n – 2 阶,共 f(n – 2)种走法
* 所以f(n)=f(n-1)+f(n-2)
* f(1) = 1 1
* f(2) = (1,1) , 2; 2
* f(3) = f(1)+f(2); 3
* f(4) = f(n-1)+f(n-2); 5
*/
if (n<=2) n else stair(n-1)+stair(n-2)
}
}
上面是递归实现,优化方法可以参考斐波那契数列的案例
汉诺塔 (Hanoi)
编程实现把 A 的 n 个盘子移动到 C(盘子编号是 [1, n] )
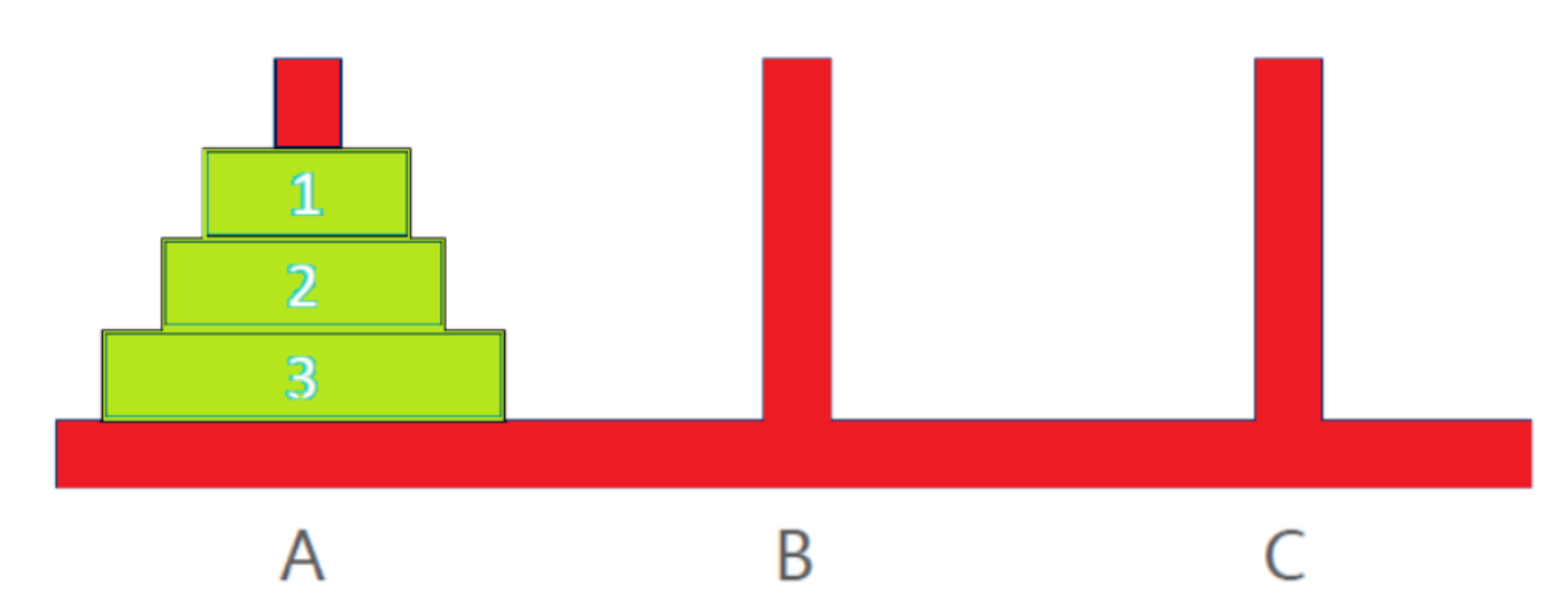
移动要求:
- 每次只能移动 1个盘子
- 大盘子必须放在小盘子下面(挪动过程中也是如此)
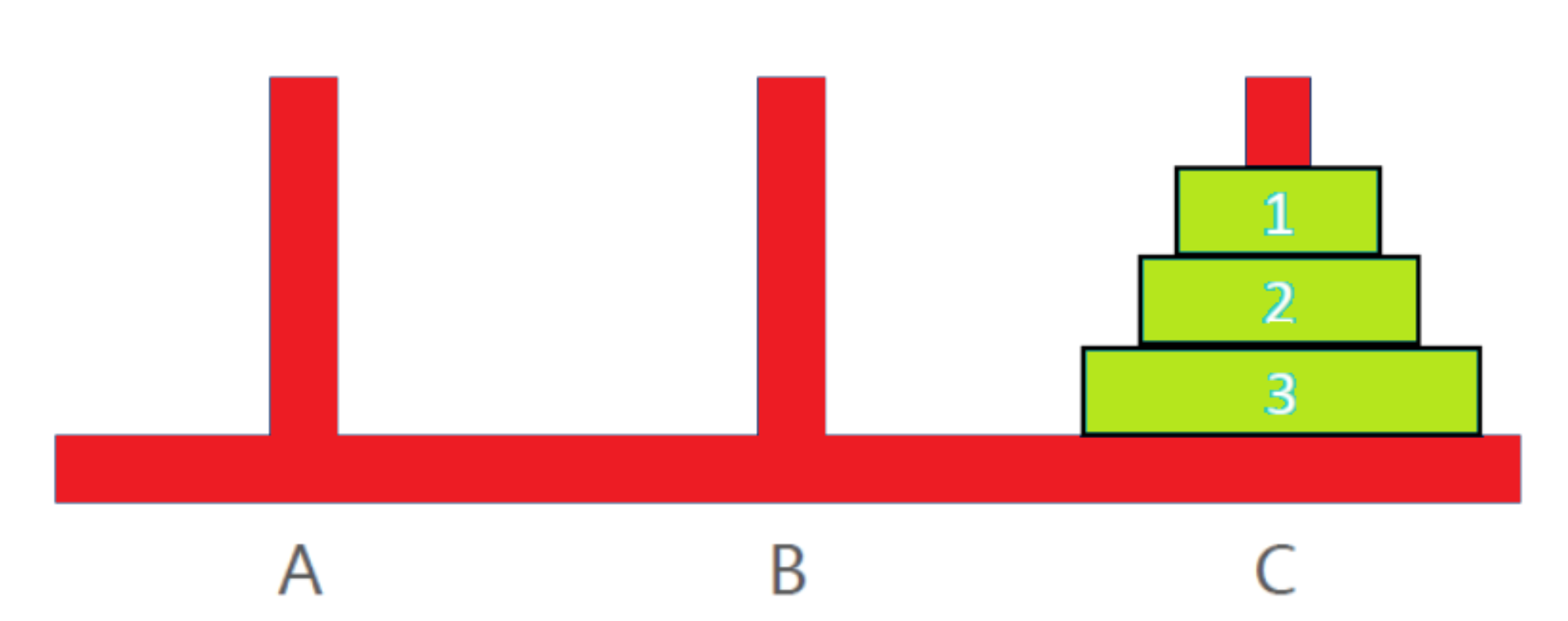
问题分析

必须将n-1个盘子移动到B柱上!!
- 如果只有一个盘子,n==1时,直接将盘子从A移动到C;
- 如果不止一个盘子,n>=2时,其实可以分为三步
- 将n-1个盘子从A移动到B
- 将编号为n的盘子从A移动到C
- 将n-1个盘子从B移动到C
第一步和第三步是相同的,不过是换了柱子
递归实现
/**
* 只打印步骤
* @param n
* @param a
* @param b
* @param c
*/
def moveHanoi(n: Int, a: String, b: String, c: String):Unit = {
// 将n-1个盘子从A移动到B
// 将编号为n的盘子从A移动到C
// 将n-1个盘子从B移动到C
if (n > 1) {
moveHanoi(n-1, a, c, b)
println(s"move $n from $a to $c")
moveHanoi(n-1, b, a, c)
}
else {
println(s"move $n from $a to $c")
}
/**
* 复杂度分析
* 时间复杂度:O(2^n)
* 空间复杂度:O(n)
**/
}
/**
* 打印步骤,并统计步数
* @param n
* @param a
* @param b
* @param c
* @param prevCount 初始值,会在递归中累加
* @return 当前循环的结果
*/
def moveHanoi(n: Int, a: String, b: String, c: String, prevCount: Int): Int = {
// 将n-1个盘子从A移动到B
// 将编号为n的盘子从A移动到C
// 将n-1个盘子从B移动到C
if (n > 1) {
val count = moveHanoi(n-1, a, c, b, prevCount) + 1
println(s"$count : move $n from $a to $c")
moveHanoi(n-1, b, a, c, count)
}
else {
val count = prevCount+1
println(s"$count : move $n from $a to $c")
count
}
}
递归百分百可以转为非递归!!
递归转非递归两种方式:
- 自己使用栈
- 考虑重复利用一组相同的变量
非递归实现hanoi问题
// 使用栈来实现,去掉递归掉用
def moveHanoi2(n: Int, a: String, b: String, c: String): Unit = {
// 将n-1个盘子从A移动到B
// 将编号为n的盘子从A移动到C
// 将n-1个盘子从B移动到C
// Boolean, Int, String, String, String
// isPrint, Int, from, middle, to
val stack = new mutable.ArrayStack[(Boolean, Int, String, String, String)]()
/**
* 使用一个stack来存需要处理的状态,遇到print就打印,遇到其他就展开后重新放回
*/
if (n > 1) {
stack.push((false, n-1, b, a, c))
stack.push((true, n, a, b, c))
stack.push((false, n-1, a, c, b))
} else {
stack.push((true, n, a, b, c))
}
while (stack.nonEmpty) {
val (isPrint, nn, from, middle, to) = stack.pop()
if (isPrint) {
println(s"move $nn from $from to $to")
} else if (nn > 1) {
stack.push((false, nn-1, middle, from, to))
stack.push((true, nn, from, middle, to))
stack.push((false, nn-1, from, to, middle))
} else {
stack.push((true, nn, from, middle, to))
}
}
}
贪心
贪心策略,也被称为贪婪策略。 什么贪心策略? 每一步都采取当前状态下最优的选择(局部最优解),从而希望推导出全局最优解
海盗运货-最优装载问题
海盗们截获了一艘装满各种各样古董的货船,每一件古董都价值连城,一旦打碎就失去了珍宝的价值 海盗船的载重 量为 W,每件古董的重量为 𝑤i,海盗们怎么做才能把尽可能多数量的古董装上海盗船? 比如 W 为 30,𝑤i 分别为 3,5,4,10,7,14,2,11
使用贪心策略解决 选择货物标准:每一次都优先选择重量最小的古董,越多越好!!
/**
1、选择重量为 2 的古董,剩重量 28
2、选择重量为 3 的古董,剩重量 25
3、选择重量为 4 的古董,剩重量 21
4、选择重量为 5 的古董,剩重量 16
5、选择重量为 7 的古董,剩重量 9
结论:按照以上顺序装载货物,并最多装载5件古董!!
*/
def piratePackage():Int = {
val capacity = 30
var goods = List(3,5,4,10,7,14,2,11)
// 按照重量升序
goods = goods.sorted
var res = capacity
var index = 0
while (res > goods(index)) {
res -= goods(index)
index+=1
}
index
}
零钱兑换
假设有 25 分、5 分、1 分的硬币,现要找给客户 41 分的零钱,如何办到硬币个数最少?
贪心策略: 每一步都优先选择面值最大的硬币 具体步骤
- 选择 25 分的硬币,剩 16 分
- 选择 5 分的硬币,剩 11 分
- 选择 5 分的硬币,剩 6 分
- 选择 5 分的硬币,剩 1 分
- 选择 1 分的硬币
最终的解是 1 枚 25 分、3 枚 5 分、1 枚 1 分的硬币,共 5 枚硬币
/**
* 零钱兑换
* 假设有 25 分、5 分、1 分的硬币,现要找给客户 41 分的零钱,如何办到硬币个数最少?
*/
def getCoins(money: Int, faces: List[Int]): Unit = {
val total = money
val sortedFaces = faces.sorted.reverse
var count = 0
var res = total
var index = 0
// 假设肯定能兑换成功
while (res != 0) {
// 如果可以兑换就兑换,不然就换小面额,继续循环
if (res >= sortedFaces(index)) {
res -= sortedFaces(index)
count+=1
println(sortedFaces(index))
} else {
index+=1
}
}
println(s"coin count: $count")
}
如果可用硬币是 5, 25, 20, 1, 则使用上面的算法无法得到最优解 (20,20,1),只能得到(25,5,5,5,1)
贪心策略的优缺点:
-
优点
- 简单、高效、不需要穷举所有可能,通常作为其他算法的辅助算法来使用
-
缺点
- 目光短浅,不从整体上考虑其他可能,每一步只采取局部最优解,不会对比其他可能性,因此贪心很少情况能获得最优解。
0-1背包问题
有 n 件物品和一个最大承重为 W 的背包,每件物品的重量是 𝑤i、价值是 𝑣i
- 在保证总重量不超过 W 的前提下,将哪几件物品装入背包,可以使得背包的总价值最大?
- 注意:每个物品只有 1 件,也就是每个物品只能选择 0 件或者 1 件,因此这类问题也被称为 0-1背包问题
使用贪婪算法可以从3个维度入手
- 价值主导:优先选择价值最高的物品放进背包
- 重量主导:优先选择重量最轻的物品放进背包
- 价值密度主导:优先选择价值密度最高的物品放进背包(价值密度 = 价值 ÷ 重量)
以下是物品列表:
| 物品序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 重量 | 35 | 30 | 60 | 50 | 40 | 10 | 25 |
| 价值 | 10 | 40 | 30 | 50 | 35 | 40 | 30 |
| 价值密度 | 0.29 | 1.33 | 0.5 | 1.0 | 0.88 | 4.0 | 1.2 |
假设背包总载重量是150,将哪几件物品装入背包,可以使得背包的总价值最大?
case class Item(weight: Double, value: Double) {
val dense:Double = value/weight
override def toString: String = s"item($weight, $value, $dense)"
}
object PackSackDemo {
def main(args: Array[String]): Unit = {
val items = List(
Item(35, 10),
Item(30, 40),
Item(60, 30),
Item(50, 50),
Item(40, 35),
Item(10, 40),
Item(25, 30)
)
println("value priority")
packSackMethod[Double](items, e=>{-e.value})
println()
println("weight priority")
packSackMethod(items, e=>{e.weight})
println()
println("dense priority")
packSackMethod(items, e=>{-e.dense})
/**
* value priority
* selected items List(item(50.0, 50.0, 1.0), item(30.0, 40.0, 1.3333333333333333), item(10.0, 40.0, 4.0), item(40.0, 35.0, 0.875))
* total value : 165.0
* res : 20
*
* weight priority
* selected items List(item(10.0, 40.0, 4.0), item(25.0, 30.0, 1.2), item(30.0, 40.0, 1.3333333333333333), item(35.0, 10.0, 0.2857142857142857), item(40.0, 35.0, 0.875))
* total value : 155.0
* res : 10
*
* dense priority
* selected items List(item(10.0, 40.0, 4.0), item(30.0, 40.0, 1.3333333333333333), item(25.0, 30.0, 1.2), item(50.0, 50.0, 1.0), item(35.0, 10.0, 0.2857142857142857))
* total value : 170.0
* res : 0
*/
}
/**
* 根据排序选择器进行排序,并从左到右开始装包
* @param items 所有物品
* @param comp 排序选择器
* @tparam B double
*/
//<:Double Double 及其子类
//>:Double Double 的父类
def packSackMethod[B<:Double](items: List[Item], comp: Item=>B): Unit = {
implicit val ord = new Ordering[B] {
override def compare(x: B, y: B): Int = x.compareTo(y)
}
val capacity = 150 //total
var res = capacity //current capacity
val sortedItems = items.sortBy(comp)
// cache selected items
val arrayBuffer = new ArrayBuffer[Item]()
for (it <- sortedItems) {
if (it.weight.intValue() <= res) {
res -= it.weight.intValue()
arrayBuffer += it
}
}
println(s"selected items ${arrayBuffer.toList}")
println(s"total value : ${arrayBuffer.map(_.value).sum}")
println(s"res : $res")
}
}
以上代码不能断定哪一个是最优解,只能说有相对较优解
分治
分治,就是分而治之。 分治的一般步骤:
1、将原问题分解成若干个规模较小的子问题(子问题和原问题的结构一样,只是规模不一样)
2、子问题又不断分解成规模更小的子问题,直到不能再分解(直到可以轻易计算出子问题的解)
3、利用子问题的解推导出原问题的解
所以:分治思想非常适合使用递归实现!! 注意:分治的适用场景中必须要求子问题之间是相互独立的,如果子问题之间不独立则需要使用动态规划实现!!
分治思想图示
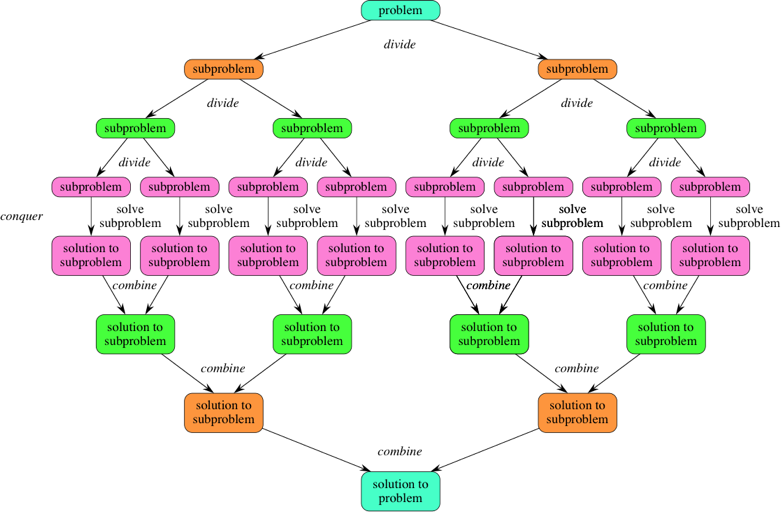
经典的排序算法,快速排序和归并排序都是使用了分治的思想
快速排序(Quick Sort)
Quick Sort分析
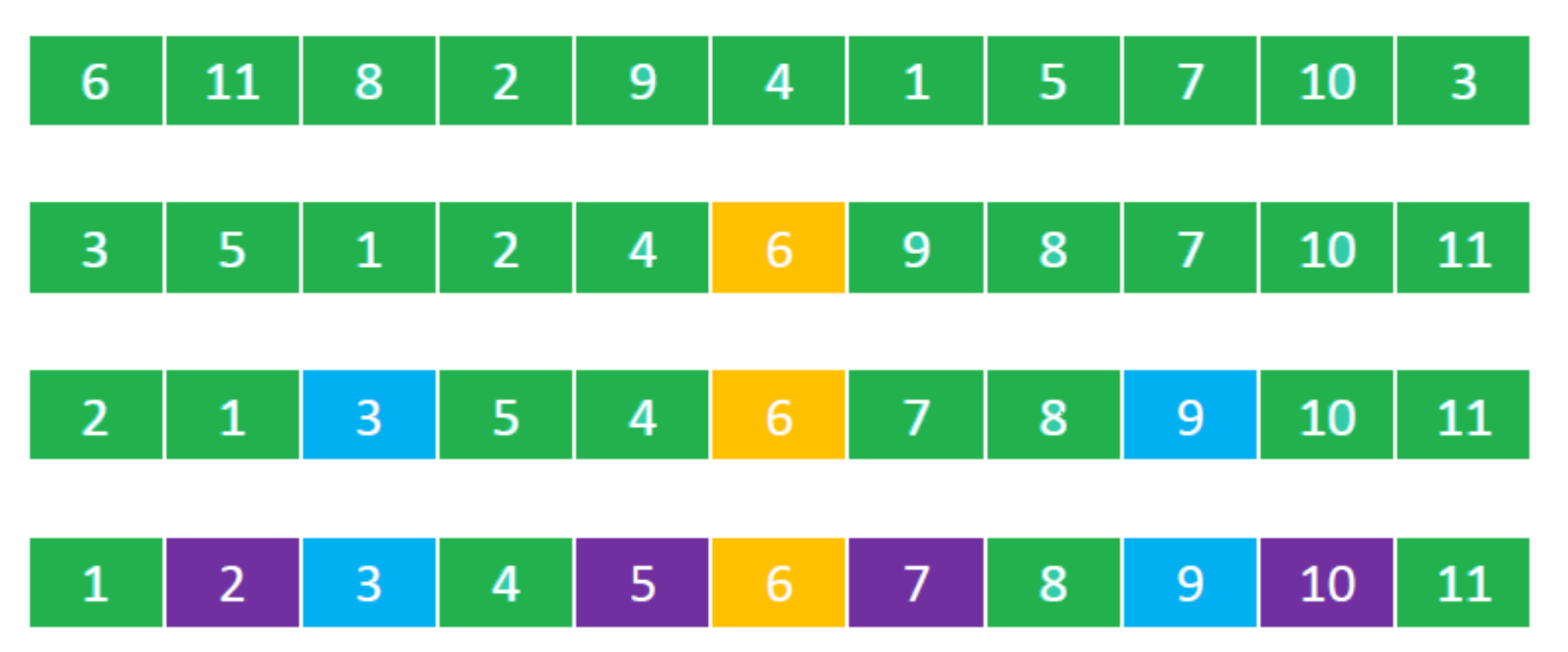
- 第一步: 从数组中选择一个轴点元素(Pivot element),一般选择0位置元素为轴点元素
- 第二步
- 利用Pivot将数组分割成2个子序列
- 将小于 Pivot的元素放在Pivot前面(左侧) ,将大于 Pivot的元素放在Pivot后面(右侧) ,等于Pivot的元素放哪边都可以(暂定放在左边)
- 第三步:对子数组进行第一步,第二步操作,直到不能再分割(子数组中只有一个元素)
Quick Sort的本质: 不断地将每一个元素都转换成轴点元素!!
代码实现
public class JavaQuickSort {
private Integer[] arr;
public static void main(String[] args) {
Integer[] array = new Integer[]{6, 2, 1, 5,6, 8,9};
JavaQuickSort js = new JavaQuickSort();
js.sort(array);
}
public void sort(final Integer[] array) {
arr = array;
// 打印排序前的数据
for (int i=0; i< arr.length; i++) {
System.out.print(arr[i]+"_");
}
System.out.println();
// 排序并打印排序后的数据
sort(0, array.length);
for (int i=0; i< arr.length; i++) {
System.out.print(arr[i]+"_");
}
System.out.println();
}
/**
* 快排实现
* @param start 开始排序的的下标
* @param end 结束排序的的下标
*/
public void sort(Integer start, Integer end) {
if (end-start < 2) return;
Integer pivot = getPivotIndex(start, end);
sort(start, pivot);
sort(pivot+1, end);
}
/**
* find define pivotElement and divide arr with pivot, return new pivot index
* @param start 开始排序的的下标
* @param end 结束排序的的下标
* @return pivot
*/
private Integer getPivotIndex(Integer start, Integer end) {
Integer pivotElement = arr[start];
end--; //point to the last index
while (start < end) {
// 小于pivot的数据往左挪
while (start<end) {
if(myCompare(pivotElement, arr[end]) < 0) {
end--;
} else {
arr[start] = arr[end];
start++;
break;
}
}
// 大于pivot的数据往右挪
while (start<end) {
if(myCompare(arr[start], pivotElement) < 0) {
start++;
} else {
arr[end] = arr[start];
end--;
break;
}
}
}
arr[start] = pivotElement;
return start;
}
// 定义比较方法,方便修改排序规则
public int myCompare(Integer t1, Integer t2) {
return t1.compareTo(t2);
}
}
- 时间复杂度
- 最坏情况:
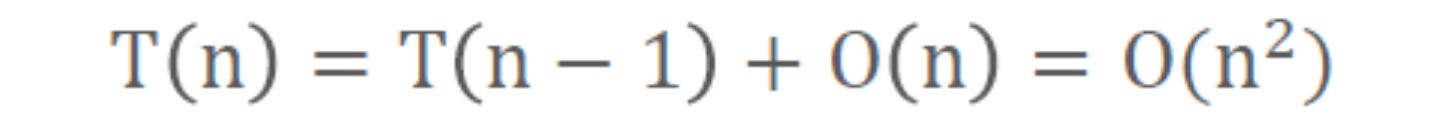
- 最好情况:
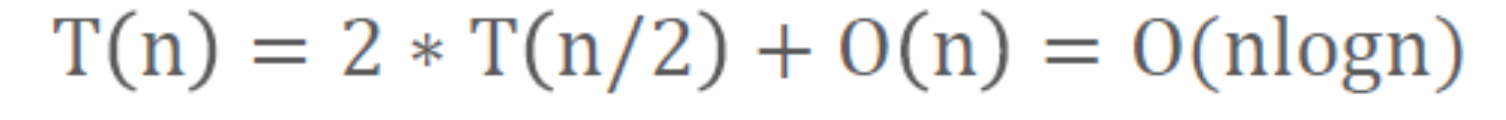
- 最坏情况:
- 空间复杂度: 由于递归调用,每次类似折半效果所以空间复杂度是O(logn)
最坏情况的例子,如下数据,如果pivot总是选第一个,时间复杂度为O(n*n)
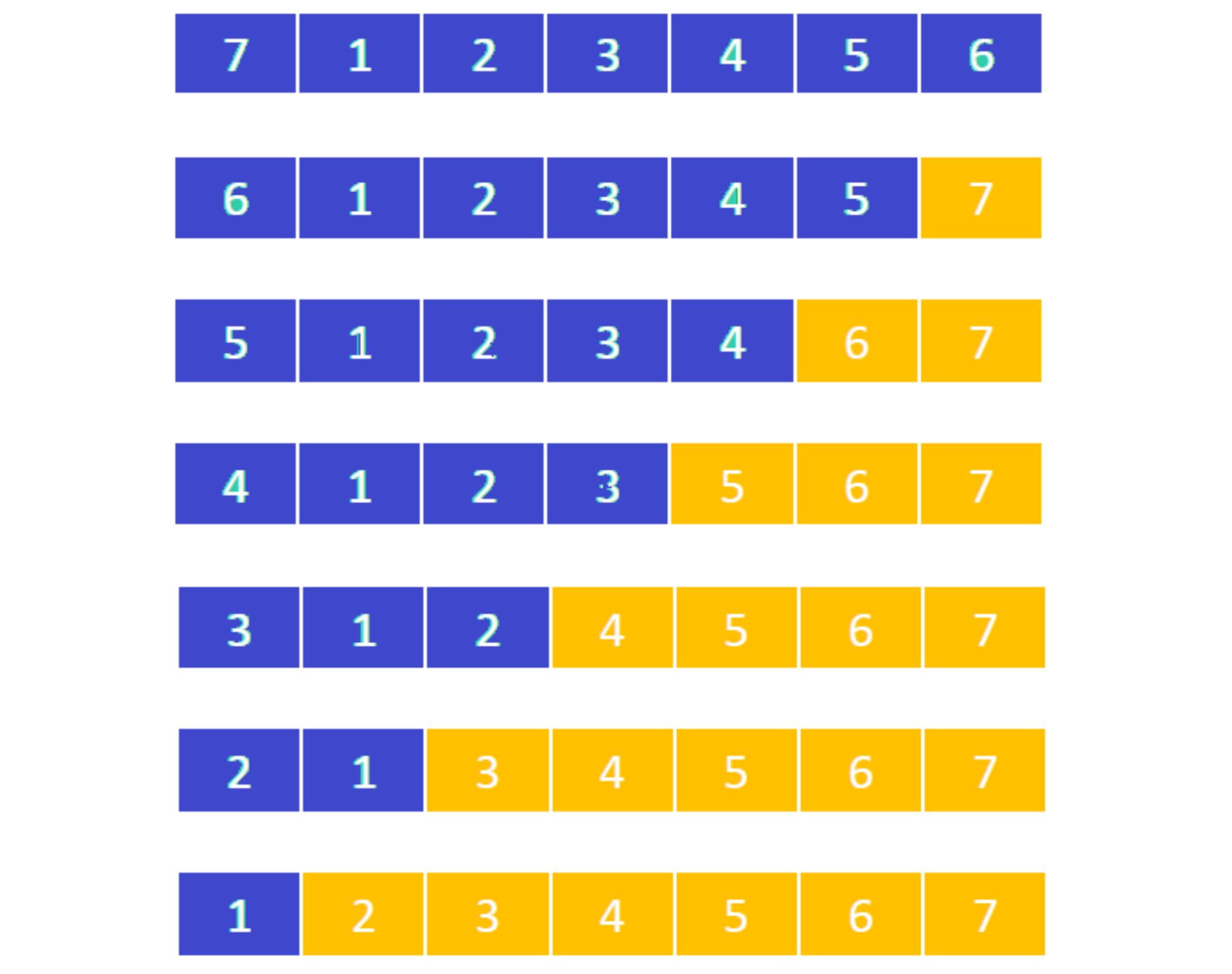
如何降低快速排序排序最坏时间复杂度产生的概率?
随机挑选一个pivot,而不是每次都选第一个元素
排序算法的稳定性
对于排序算法还有一个评价指标就是稳定性!!
什么是排序算法的稳定性?
如果相等的2个元素,在排序前后的相对位置保持不变,则该算法是稳定的排序算法!!
快排是不稳定的排序
举个例子
如果a=b
排序前:5, 1, 2𝑎, 4, 7, 2𝑏
稳定的排序: 1,2𝑎,2𝑏 ,4,5,7
不稳定的排序:1, 2𝑏 , 2𝑎, 4, 5, 7
对于数值类型的排序而言,算法的稳定性没有意义,但是对于自定义对象的排序,排序算法的稳定性是会影响最终结果的!!
动态规划
动态规划,简称为DP。 动态规划是求解最优化问题的一种常用策略。
动态规划使用步骤:
- 递归(自顶向下,出现了重叠子问题)
- 递推(自底向上,循环)
定义:
Dynamic Programming is a method for solving a complex problem by breaking it down into a
collection of simpler subproblems, solving each of those subproblems just once, and
storing their solutions.
动态规划策略可以解决哪些问题?
这类问题通常具有两个特点:
* 最优化问题(最优子结构问题):通过求解子问题的最优解,可以获得原问题的最优解
* 无后效性
无后效性
无后效性是指某阶段的状态一旦确定后,后续状态的演变不再受此前各状态及决策的影响(未来与过去无 关);在推导后面阶段的状态时,只关心前面阶段的具体状态值,不关心这个状态是怎么一步步推导出! (昨天的过失不会影响今天的决策)
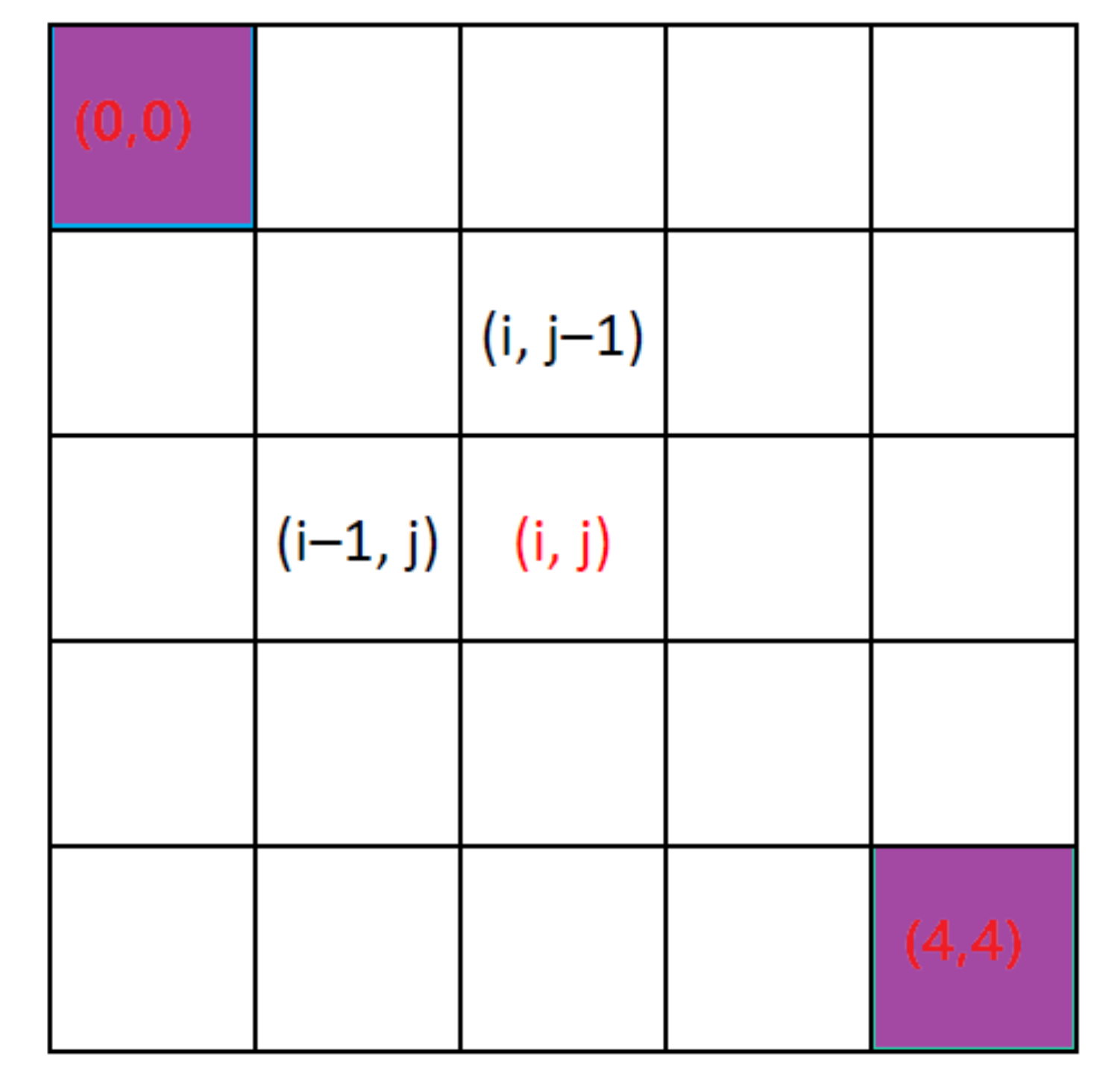
- 从起点(0, 0)走到终点(4, 4)一共有多少种走法?只能向右、向下走
- 假设 dp(i, j) 是从(0, 0)走到(i, j)的走法
- dp(i, 0) = dp(0, j) = 1
- dp(i, j) = dp(i, j – 1) + dp(i – 1, j)
总结:推导 dp(i, j) 时只需要用到 dp(i, j – 1)、dp(i – 1, j) 的值 不需要关心 dp(i, j – 1)、dp(i – 1, j) 的值是怎么求出来的
有后效性

规则:可以向左、向右、向上、向下走,并且同一个格子不能走 2 次
有后效性:
- dp(i, j) 下一步要怎么走,还要关心上一步是怎么来的
- 还需要考虑 dp(i, j – 1)、dp(i – 1, j) 是怎么来的
实现步骤
- 定义状态:状态指的是原问题,子问题的解,例如dp(i)
- 设定初始状态:问题的边界,比如设置dp(0)的值
- 确定状态转移方程:如确定 dp(i) 和 dp(i – 1) 的关系
零钱兑换
假设有25分、20分、5分、1分的硬币,现要找给客户41分的零钱,如何办到硬币个数最少? 此前贪心策略求解结果是5枚硬币,并非是最优解!
思路:
-
定义状态 dp(n):凑到 n 分需要的最少硬币个数
-
设定初始状态
dp(25)=dp(20)=dp(5)=dp(1)=1
-
确定状态转移方程
- 如果第 1 次选择了 25 分的硬币,那么 dp(n) = dp(n – 25) + 1
- 如果第 1 次选择了 20 分的硬币,那么 dp(n) = dp(n – 20) + 1
- 如果第 1 次选择了 5 分的硬币,那么 dp(n) = dp(n – 5) + 1
- 如果第 1 次选择了 1 分的硬币,那么 dp(n) = dp(n – 1) + 1
- 所以 dp(n) = min { dp(n – 25), dp(n – 20), dp(n – 5), dp(n – 1) } + 1
//递归(自顶向下,出现了重叠子问题)
def coinChange1(n: Int):Int = {
// 边界状态
if (n < 1) return Int.MaxValue
// 设定初始状态
if(List(1, 5, 20, 25).contains(n)) return 1
// 状态转移方程
List(
coinChange1(n-1),
coinChange1(n-5),
coinChange1(n-20),
coinChange1(n-25)
).min + 1
}
这种递归方式会存在大量重复计算,时间复杂度是比较高的!!
优化一
使用递推方式实现,从小计算到大。
// 递推(自底向上,循环)
def coinChange2(n: Int):Int = {
if (n < 1) return Int.MaxValue
if(List(1, 5, 20, 25).contains(n)) return 1
val dp = Array.fill(n+1)(Int.MaxValue)
dp(1) = 1
dp(5) = 1
dp(20) = 1
dp(25) = 1
for (i <- 1 to n) {
if (i > 25) {
dp(i) = List(dp(i-1), dp(i-5), dp(i-20), dp(i-25)).min+1
} else if (i > 20) {
dp(i) = List(dp(i-1), dp(i-5), dp(i-20)).min+1
} else if (i > 5) {
dp(i) = List(dp(i-1), dp(i-5)).min+1
} else if (i > 1) {
dp(i) = dp(i-1)+1
}
}
dp(n)
}
通用方案
/**
* 动态规划实现零钱兑换
* @param amount 需要兑换的总额
* @param coins 币的类型
* @return 最小币数,如果不存在就返回-1
*/
def coinChange4(amount: Int, coins: List[Int]):Int = {
if (amount < 1 || coins == null || coins.isEmpty) return -1
val dp = Array.fill(amount+1)(0)
for (i <- 1 to amount) {
var min = Int.MaxValue
coins.foreach { face =>
if (i >= face && dp(i-face) >= 0) {
min = Math.min(dp(i-face), min)
}
}
if (min == Int.MaxValue) {
dp(i) = -1
} else {
dp(i) = min+1
}
}
dp(amount)
}
最大的连续子序列和
给定一个长度为 n 的整数序列,求它的最大连续子序列和
–2、1、–3、4、–1、2、1、–5、4 的最大连续子序列和是 4 + (–1) + 2 + 1 = 6
-
定义状态
dp(i) 是以 nums[i] 结尾的最大连续子序列和(nums是整个序列)
-
初始状态 dp(0)=nums[0]
-
状态转移方程
如果以 nums[0] –2 结尾,则最大连续子序列是 –2,所以 dp(0) = –2 如果以 nums[1] 1 结尾,则最大连续子序列是 1,所以 dp(1) = 1 如果以 nums[2] –3 结尾,则最大连续子序列是 1、–3,所以 dp(2) = dp(1) + (–3) = –2 如果以 nums[3] 4 结尾,则最大连续子序列是 4,所以 dp(3) = 4 如果以 nums[4] –1 结尾,则最大连续子序列是 4、–1,所以 dp(4) = dp(3) + (–1) = 3 如果以 nums[5] 2 结尾,则最大连续子序列是 4、–1、2,所以 dp(5) = dp(4) + 2 = 5 如果以 nums[6] 1 结尾,则最大连续子序列是 4、–1、2、1,所以 dp(6) = dp(5) + 1 = 6 如果以 nums[7] –5 结尾,则最大连续子序列是 4、–1、2、1、–5,所以 dp(7) = dp(6) + (–5) = 1 如果以 nums[8] 4 结尾,则最大连续子序列是 4、–1、2、1、–5、4,所以 dp(8) = dp(7) + 4 = 5- 如果 dp(i – 1) ≤ 0,那么 dp(i) = nums[i]
- 如果 dp(i – 1) > 0,那么 dp(i) = dp(i – 1) + nums[i]
最终解:
最大连续子序列和是所有 dp(i) 中的最大值 max { dp(i) },i ∈ [0, nums.length)
def maxSubSequence2(list: List[Int]): Int = {
/**
* dp(i) 是以 nums[i] 结尾的最大连续子序列和(nums是整个序列)
* dp(0) = nums[0]
* 如果 dp(i – 1) ≤ 0,那么 dp(i) = nums[i]
* 如果 dp(i – 1) > 0,那么 dp(i) = dp(i – 1) + nums[i]
*
* dp(i) = 最大连续子序列和是所有 dp(i) 中的最大值 max { dp(i) },i ∈ [0, nums.length)
*/
if (list == null || list.isEmpty) return 0
val dp = new Array[Int](list.size)
dp(0) = list.head
for (i <- 1 until list.size) {
dp(i) = list(i) + (if(dp(i-1)<=0) 0 else dp(i-1))
}
dp.max
}
优化方案,使用变量代替数组
// 使用变量代替数组
def maxSubSequence3(list: List[Int]): Int = {
/**
* dp(i) 是以 nums[i] 结尾的最大连续子序列和(nums是整个序列)
* dp(0) = nums[0]
* 如果 dp(i – 1) ≤ 0,那么 dp(i) = nums[i]
* 如果 dp(i – 1) > 0,那么 dp(i) = dp(i – 1) + nums[i]
*
* dp(i) = 最大连续子序列和是所有 dp(i) 中的最大值 max { dp(i) },i ∈ [0, nums.length)
*/
if (list == null || list.isEmpty) return 0
var lastSum = list.head
var max = lastSum
for (i <- 1 until list.size) {
lastSum = list(i) + (if(lastSum<=0) 0 else lastSum)
max = Math.max(max, lastSum)
}
max
}
最长公共子序列(Longest Common Subsequence,LCS)
计算两个序列的最长公共子序列长度
[1, 3, 5, 9, 10] 和 [1, 4, 9, 10] 的最长公共子序列是 [1, 9, 10],长度为 3
思路分析
假设 2 个序列分别是 nums1、nums2
i ∈ [0, nums1.length]
j ∈ [0, nums2.length]
-
定义状态方程
dp(i, j) 是 [nums1 前 i 个元素] 与[nums2 前 j 个元素] 的最长公共子序列长度
-
定义初始值
dp(i, 0)、dp(0, j) 初始值均为 0
-
定义状态转移方程
-
假设 nums1[i – 1] = nums2[j – 1],那么 dp(i, j) = dp(i – 1, j – 1) + 1
-
假设 nums1[i – 1] ≠ nums2[j – 1],那么 dp(i, j) = max { dp(i – 1, j), dp(i, j – 1) }
-
递推实现
// 二维数组实现
def commonNumsSubsequence2(list1: List[Int], list2: List[Int]):Unit = {
/**
* 1. 状态函数
* dp(i)(j) 表示list1的前i个元素 和 list2的前j个元素的最长子序列长度
*
* 2. 初始状态
* dp(i)(0) = 0
* dp(0)(j) = 0
*
* 3. 状态转移函数
* 假设 list1[i – 1] = list2[j – 1],那么 dp(i, j) = dp(i – 1, j – 1) + 1
* 假设 list1[i – 1] ≠ list2[j – 1],那么 dp(i, j) = max { dp(i – 1, j), dp(i, j – 1) }
*/
if (list1 == null || list2 == null || list1.isEmpty || list2.isEmpty) return 0
val dp = Array.ofDim[Int](list1.size+1, list2.size+1)
for (i <- 1 to list1.size; j <- 1 to list2.size) {
if (list1(i-1) == list2(j-1)) {
dp(i)(j) = dp(i-1)(j-1) + 1
} else {
dp(i)(j) = Math.max(dp(i-1)(j), dp(i)(j-1))
}
}
dp.last.last
}
优化数据结构
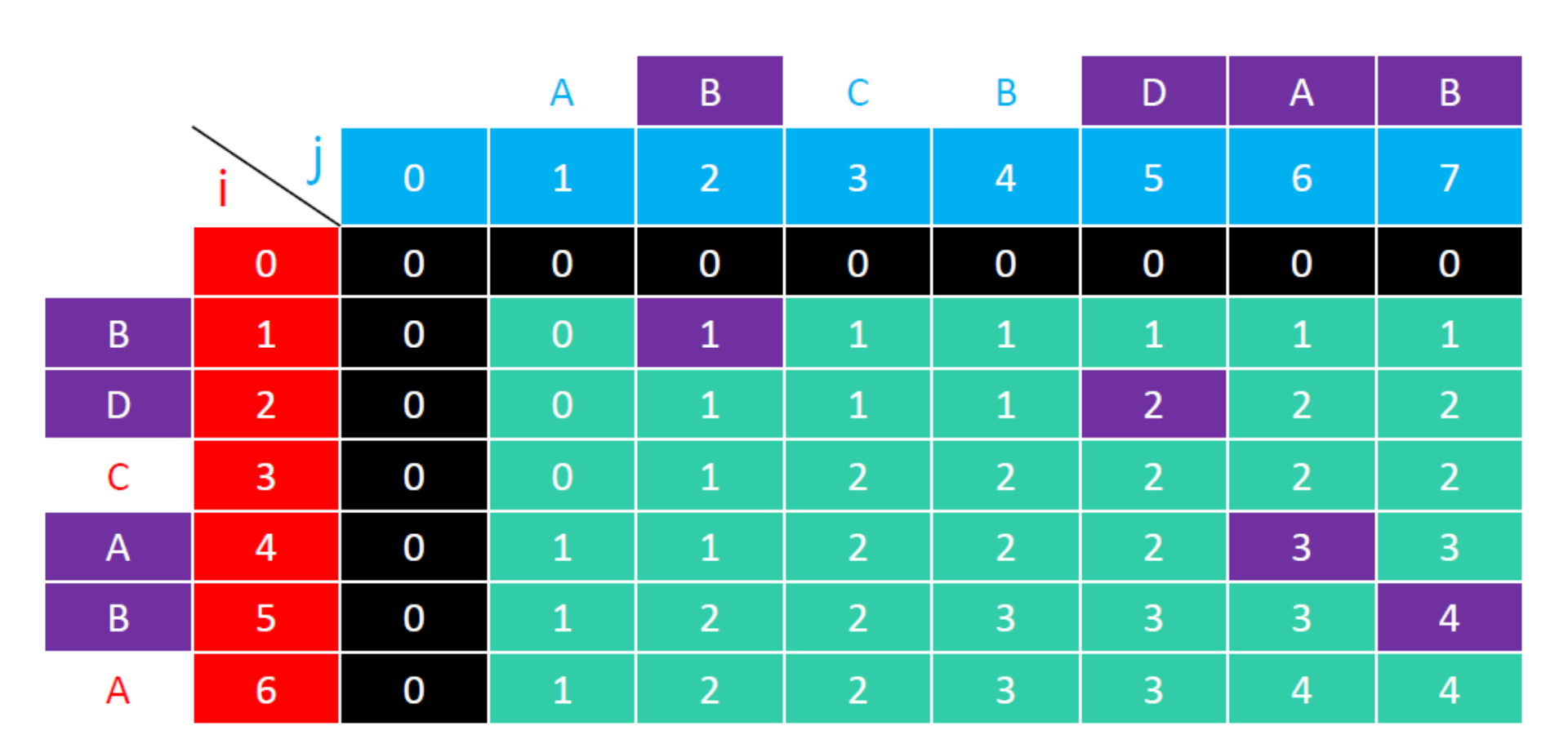
其实上面的递推过程,每次只需要用到上一行的数据,所以可以改用一维数组来存状态
// 一维数组实现
def commonNumsSubsequence3(list1: List[Int], list2: List[Int]):Unit = {
if (list1 == null || list2 == null || list1.isEmpty || list2.isEmpty) return
val dp = new Array[Int](list2.size+1)
// 处理list2有重复元素,且和list1相等的场景
// 方法一
// for (i <- 1 to list1.size) {
// println()
// var isFound = false
// for (j <- 1 to list2.size) {
// if (list1(i-1) == list2(j-1) && !isFound) {
// dp(j) = dp(j-1) + 1
// isFound = true
// } else {
// dp(j) = Math.max(dp(j), dp(j-1))
// }
// print(dp(j) + ", ")
// }
// }
// 方法二
for (i <- 1 to list1.size) {
println()
var tmp = 0
for (j <- 1 to list2.size) {
//暂存上一次循环左上角的值
val leftTop = tmp
tmp = dp(j)
if (list1(i-1) == list2(j-1)) {
dp(j) = leftTop + 1
} else {
dp(j) = Math.max(dp(j), dp(j-1))
}
}
}
dp.last
}
0-1背包问题
有 n 件物品和一个最大承重为 W 的背包,每件物品的重量是 𝑤i、价值是 𝑣i
在保证总重量不超过 W 的前提下,将哪几件物品装入背包,可以使得背包的总价值最大?
注意:每个物品只有 1 件,也就是每个物品只能选择 0 件或者 1 件,因此这类问题也被称为 0-1背包问题
动态规划步骤
使用样例类Item封装数据items,最大承重capacity = 10
case class Item(weight: Int, value: Int)
val items = List(
Item(2, 6),
Item(2, 3),
Item(6, 5),
Item(5, 4),
Item(4, 6)
)
val capacity = 10
-
定义状态方程 dp( i, j ) 是 最大承重为 j、有前 i 件物品可选时的最大总价值,i ∈ [0, n],j ∈ [0, W]
-
初始状态 dp( i, 0 )、dp( 0, j ) 初始值均为 0
-
状态转移方程 dp( i, j )=dp( i-1, j-1 ) 如果只剩最后一件物品时,有两种情况
- 不选择该物品:dp( i, j ) = dp( i-1, j )
- 选择该物品:dp( i, j ) = values[i] + dp( i-1, j-weights[i] )
dp( i, j )返回的是最大总价值 max{ dp( i-1, j ), values[i] + dp( i-1, j - weights[i] ) }
- 如果 j < weights[i – 1],那么 dp(i, j) = dp(i – 1, j)
- 如果 j ≥ weights[i – 1],那么 dp(i, j) = max{ dp( i-1, j ), values[i] + dp( i-1, j - weights[i] ) }
// 使用 I * J 二维数据缓存数据
def packSack1(items: List[Item], capacity: Int):Unit = {
/**
* * 定义状态方程
* dp(i, j) 是 最大承重为 j、有前 i 件物品可选 时的最大总价值,i ∈ [0, n],j ∈ [0, W]
*
* * 初始状态
* dp(i, 0)、dp(0, j) 初始值均为 0
*
* * 状态转移方程
* dp(i,j)=dp(i-1,j-1)
* 如果只剩最后一件物品时,有两种情况
* * 不选择该物品:dp(i,j)=dp(i-1,j)
* * 选择该物品:dp(i,j)=values[i]+dp(i-1,j-weights[i])
* dp(i,j)返回的是最大总价值 max(dp(i-1,j),values[i]+dp(i-1,j-weights[i]))
* 如果 j < weights[i – 1],那么 dp(i, j) = dp(i – 1, j)
* 如果 j ≥ weights[i – 1],那么 dp(i, j) = max { dp(i – 1, j), dp(i – 1, j – weights[i – 1]) + values[i – 1] }
*/
val dp: Array[Array[Int]] = Array.ofDim[Int](items.size+1, capacity+1)
for (i <- 1 to items.size; j <- 1 to capacity) {
val it = items(i-1)
if (j < it.weight) {
dp(i)(j) = dp(i-1)(j)
} else {
dp(i)(j) = Math.max(dp(i-1)(j), dp(i-1)(j-it.weight)+it.value)
}
}
dp.foreach(e => println(e.toList))
printSelectItems(items, dp)
}
打印选中的商品
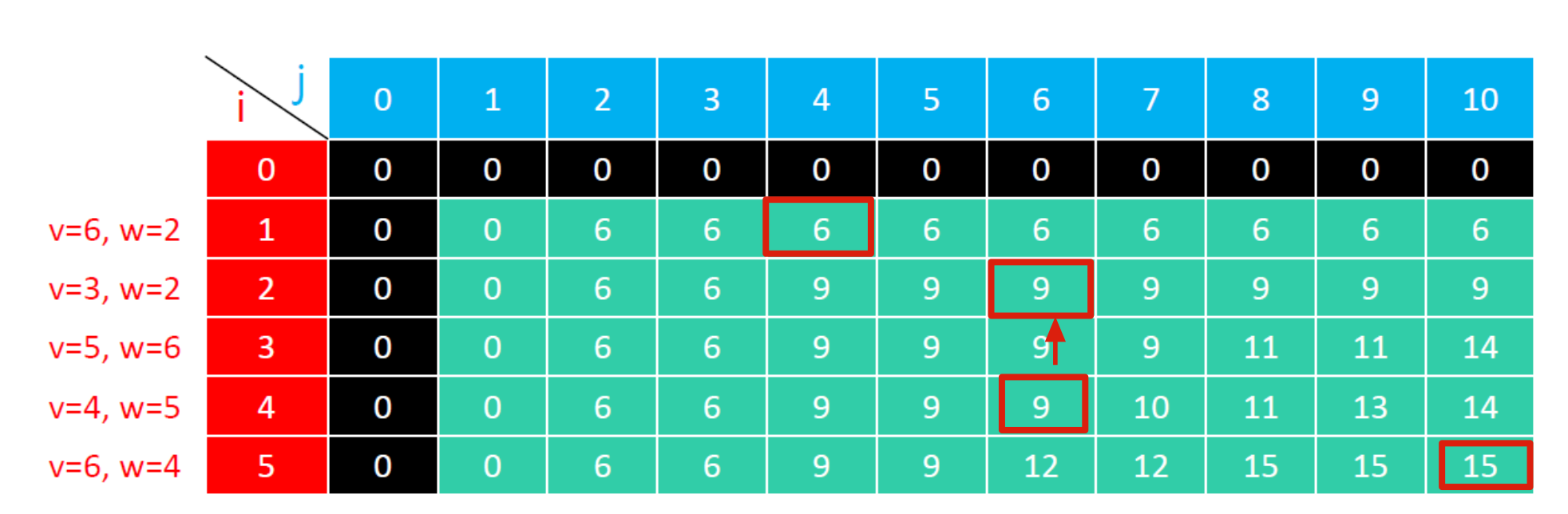
二维dp的结果如上表,从最后列往最后一个元素,可以推算出,每次选中的物品
- 当前列dp(i)(j) > dp(i-1)(j)
- 说明选中了物品 i,且可以反推出 dp(i,j)=values[i]+dp(i-1,j-weights[i])
- 上一个选中的物品可能是 i-1, 接下来需要判断 dp(i-1,j-weights[i]) > dp(i-2,j-weights[i]) ?
- 当前列dp(i)(j) == dp(i-1)(j) * 说明没有选中 i ,判断 dp(i-1)(j) == dp(i-2)(j) ?
/**
* 打印选中的商品
* @param items 完整的商品列表
* @param dp 动态规划结果表
*/
def printSelectItems(items: List[Item], dp: Array[Array[Int]]): Unit = {
var i = dp.length-1
var j = dp.head.length-1
val selectedItems = new ArrayBuffer[Item]()
while (i > 0 && j > 0) {
if (dp(i)(j) > dp(i-1)(j)) {
selectedItems += items(i-1)
j -= items(i-1).weight
}
i -= 1
}
println("selected items")
println(selectedItems.reverse.toList)
}
数据结构优化
// 优化数据结构; 使用 2 * J 二维数据缓存数据
def packSack2(items: List[Item], capacity: Int):Unit = {
val dp = Array.ofDim[Int](2, capacity+1)
for (i <- 1 to items.size) {
val current = i%2
val last = 1-current
val it = items(i-1)
for (j <- 1 to capacity) {
if (j < it.weight) {
dp(current)(j) = dp(last)(j)
} else {
dp(current)(j) = Math.max(dp(last)(j), dp(last)(j-it.weight)+it.value)
}
}
println(dp(current).toList)
}
println(dp.last.last)
}
// 优化数据结构; 使用 一维数据缓存数据
def packSack3(items: List[Item], capacity: Int):Unit = {
val dp = new Array[Int](capacity+1)
for (i <- 1 to items.size) {
val it = items(i-1)
// WARN: 这里需要逆序,防止数据被覆盖
for (j <- Range(capacity, it.weight-1, -1)) {
dp(j) = Math.max(dp(j), dp(j-it.weight)+it.value)
}
println(dp.toList)
}
println(dp.last)
}